Основные законы алгебры логикиЗакон нулевого множества
1)0 * Х = 0
2)0+ Х= Х
0 – разрыв цепи Закон универсального множества
1)1* Х=Х
2)1+Х=1
Закон повторения 1)Х*Х*….*Х=Х
2)Х+Х+…+Х=Х
Закон дополнительности 1)Х*Х=0
2)Х+Х=1
Переместительный закон 1)Х1+Х2=Х2+Х1
2)Х1*Х2=Х2*Х1
Сочетательный закон 1)Х1*Х2*Х3=(Х1*Х2)*Х3=(Х1*Х3)*Х2 2)Х1+Х2+Х3=(Х1+Х2)+Х3=(Х2+Х3)+Х1
Распределительный закон Х1*(Х2+Х3)=Х1*Х2+Х1*Х3 Закон инверсии (Закон Де Моргана) 1)
2)
Закон двойной инверсии
Все законы применяют для минимизации схем управлений(меньше контактов, меньше реле)для повышения надёжности.
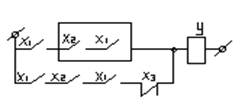
Пример: У=Х1*Х2*Х1+Х3(Х2*Х1*Х3)
1.По закону инверсии минимизируем схему. У=Х1*(Х2+Х1)+Х3(Х2*Х1*Х3) 2.По распределительному закону минимизируем схему У=Х1*Х2+Х1*Х1+Х3(Х2*Х1*Х3) 3.По закону дополнительности минимизируем схему. У=Х1*Х2+0+Х3*Х2*Х1*Х3 У=Х1*Х2
|
= 
+ 
+ 
= 
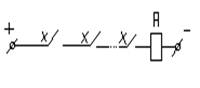
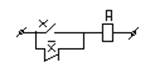
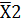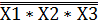=Х1+Х2+Х3
=Х1*Х2*Х3
