Замечания
1. Если система дифференциальных уравнений не интегрируется в элементарных функциях, то решение задачи в данном пособии заканчивается составлением дифференциальных уравнений движения системы. 2. Если по условию задачи требуется определить обобщенные ускорения
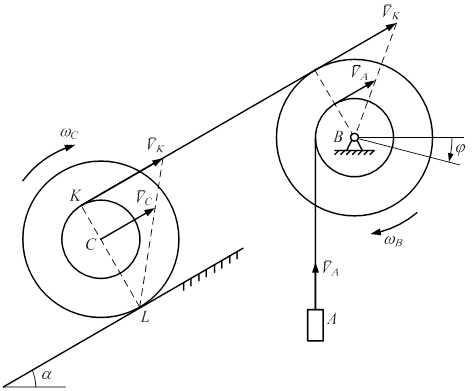
Задача 1.1. Система на рис. 1.11 состоит из груза A, ступенчатого барабана B и катушки C. Постоянный момент M = 12 Pr вращает барабан B, наматывая на него два троса, поднимающих груз A и катушку C, катящуюся без проскальзывания по наклонной плоскости, образующей с горизонтом угол a.
Рис. 1.11 Вес груза A равен 5 P, вес барабана B равен P, R = 2 r. Радиус инерции барабана B относительно его оси вращения – r. Вес катушки C равен 2 P, радиус инерции катушки относительно оси ее симметрии – Пренебрегая весом тросов и сопротивлением движению, составить дифференциальное уравнение движения системы и определить из этого уравнения угловое ускорение барабана B. Решение. На систему (рис. 1.11) действуют активные силы: PA, PB, PC и момент M. Система имеет одну степень свободы, так как закрепление точки A, движущейся по прямой, ведет к остановке всей системы. За обобщенную координату возьмем угол j поворота барабана B. Определим кинетическую энергию системы:
T = TA + TB + TC.
По формулам (2)... (4) прил. 2 имеем
Выразим VA, w B, w C, VC через
Подставляя эти данные в T и учитывая, что
после преобразований получим
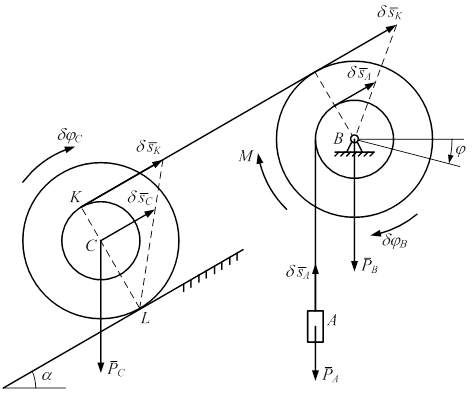
Определим обобщенную силу Q. Малое приращение обобщенной координаты dj B и соответствующие возможные перемещения объектов системы показаны на рис. 1.13. Обратите внимание на аналогию между картиной скоростей системы (рис. 1.12) и картиной возможных перемещений (рис. 1.13). Составим выражение суммы работ активных сил на возможных перемещениях:
Из анализа рис. 1.13 следует, что
Рис. 1.12
Рис. 1.13
Подставляя эти результаты в
Для составления дифференциального уравнения движения системы вначале установим, что
Подставляя эти результаты и найденное ранее Q в уравнение (1.1), после преобразований получим угловое ускорение барабана B
Далее предлагается самостоятельно решить задачу 1.2.
Ответ: aA = (P – 0, 5 Q sin a) g (P + 0, 875 Q)-1.
Задача 1.3. Система на рис. 1.15 состоит из диска D и стержня AB, соединенных между собой шарниром A. Диск D может вращаться относительно горизонтальной оси O, перпендикулярной его плоскости. Сплошной однородный диск D имеет вес P, радиус r. Тонкий однородный стержень AB имеет вес 2 P, длину 4 r. Составить дифференциальные уравнения движения системы под действием сил тяжести. Сопротивлением движению пренебречь. Решение. Активные силы системы – силы тяжести PD и PAB. Для определения числа степеней свободы системы (рис. 1.15) закрепим вращающийся диск D. После этого стержень AB сможет вращаться вокруг неподвижной оси A. Если закрепить еще и стержень AB, то получим неподвижную систему. Это значит, что система имеет две степени свободы. В качестве обобщенных координат системы возьмем углы j и q.
Рис. 1.15 Рис. 1.16
Определим кинетическую энергию системы: T = TD + TAB. По формулам (3) и (4) прил. 2 имеем
Выразим w D, w AB и VC через обобщенные скорости
где
Эту формулу можно также получить, считая, что VС – диагональ параллелограмма, построенного на скорости полюса А ( Далее, учитывая, что
получим после преобразований следующее выражение
Определим обобщенные силы Q 1 и Q 2 (рис. 1.16). Сумму работ активных сил PD и PAB будем определять, используя координатную форму работы силы (1.3б)
Из анализа рис. 1.16 следует:
По формулам (7) прил. 1 имеем
Определение Q 1. Дадим системе первое возможное перемещение, когда dj > 0, dq = 0; из формул (л) имеем
далее находим
по формуле (1.4) Определение Q 2. Дадим системе второе возможное перемещение, когда dj = 0, dq > 0; из формул (л) имеем
далее находим
по формуле (1.4) Для составления дифференциальных уравнений движения системы вначале установим, что
Подставив эти результаты, а также найденные ранее Q 1 и Q 2 в уравнения (1.1), после преобразования получим искомые дифференциальные уравнения движения системы:
Далее предлагается самостоятельно решить задачу 1.4.
Ответ: аА = P sin 2a g (3(P + Q) – 2 P cos 2a)-1, aB/A = 2 (P + Q) sin a g (3(P + Q) – 2 P cos 2a)-1.
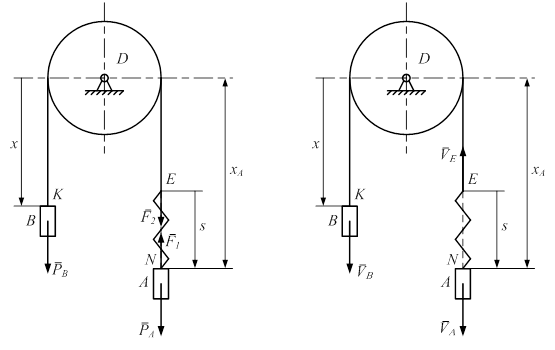
Задача 1.5. Система на рис 1.18 состоит из двух грузов A и B. Грузы соединены нерастяжимой нитью KE и пружиной EN, как показано на рис. 1.18. Вес груза A равен P, вес груза B равен 2 P. Коэффициент жесткости пружины равен с, длина недеформированной пружины равна
Решение. На систему действуют активные силы: PA = P, PB = 2 P и упругие силы пружины F 1 = F 2 = c (s – Система имеет две степени свободы, так как для остановки ее нужно закрепить две точки A и B, движущиеся по вертикали. В качестве обобщенных координат возьмем xB = x и s. Отметим, что координата s определяет длину пружины в произвольном положении. Определим кинетическую энергию системы: T = TA + TВ. По формуле (2) прил. 2 имеем
Выразим VA и VB через обобщенные скорости Из анализа рис. 1.19 следует:
Рис. 1. 18 Рис. 1.19
Подставив эти значения в T и учитывая, что
получим
Определим обобщенные силы Q 1 и Q 2. Определение Q 1. Дадим системе первое возможное перемещение, (рис. 1.20, а), когда d x > 0, d s = 0; при этом груз B переместится вниз на расстояние d x, точка E и груз A переместятся вверх на такое же расстояние
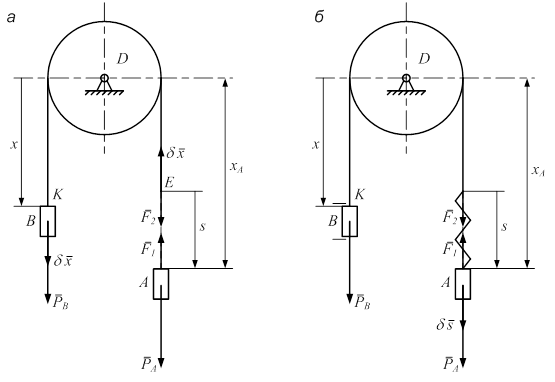
затем по формуле (1.4) с учетом заданных значений сил получим Q 1 = P. Определение Q 2. Дадим системе второе возможное перемещение, когда d x = 0, d s > 0 (рис. 1.20, б); при этом груз B и точка E останутся неподвижными, а груз A переместится вниз на расстояние d s
затем по формуле (1.4) получим
Рис. 1.20
Для составления дифференциальных уравнений движения данной системы вначале установим, что
Подставляя эти результаты, а также найденные ранее обобщенные силы Q 1 и Q 2 в уравнения (1.1), получим искомые уравнения движения рассматриваемой системы
Решая совместно эти уравнения, получим
Для интегрирования уравнения (н) произведем замену переменной s на u так, чтобы это уравнение приняло вид дифференциального уравнения гармонических колебаний
где Характеристическое уравнение, соответствующее дифференциальному уравнению (п), имеет мнимые корни. Поэтому решение уравнения (п) запишем в виде
Возвращаясь к переменной s, получим
Из начальных условий
Тогда уравнение (р) примет вид
Подставляя (с) в (м), после преобразований получим
Интегрируя это дифференциальное уравнение с учетом заданных условием задачи начальных условий, найдем уравнение движения груза A:
Далее предлагается самостоятельно решить задачу 1.6.
Задача 1.6. На однородный сплошной диск А весом Р и радиусом r (рис. 1.21) намотана нерастяжимая нить. Точка В вертикального участка этой нити соединена с нижним концом пружины ВD, верхний конец которой неподвижен. Коэффициент жесткости пружины равен с. В начальный момент диск находился в покое, пружина длиной
Ответ: x = xo + g /3(t 2 + 1/ k 2 (1 – coskt)), s = где k = 3 gc/P, g – ускорение свободного падения.
|

 , то система дифференциальных уравнений решается как алгебраическая система уравнений.
, то система дифференциальных уравнений решается как алгебраическая система уравнений.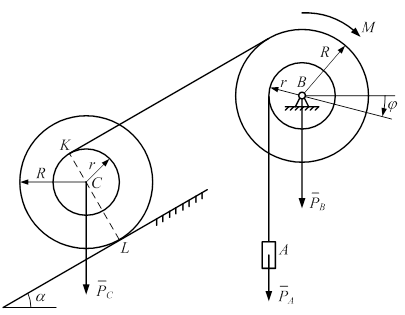
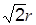 .
. .
.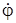 (рис. 1.12):
(рис. 1.12): 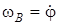 ,
,  ,
, 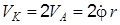 . Мгновенный центр скоростей катушки находится в точке L, поэтому
. Мгновенный центр скоростей катушки находится в точке L, поэтому .
.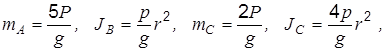
 .
.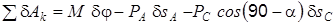 .
. .
.
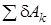 и учитывая заданные условием задачи величины сил, после преобразований получим
и учитывая заданные условием задачи величины сил, после преобразований получим .
.
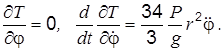
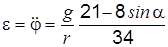 .
. Задача 1.2. Груз А весом Р посредством нерастяжимой нити, переброшенной через блок В, приводит в движение каток С, который катится без проскальзывания по наклонной плоскости (рис. 1.14). Каток и блок – однородные сплошные диски одинакового веса Q и радиуса r. Наклонная плоскость образует с горизонтом угол a. Следует составить дифференциальное уравнение движения системы под действием сил тяжести и затем определить из полученного уравнения ускорение груза А. За обобщенную координату рекомендуется взять xA.
Задача 1.2. Груз А весом Р посредством нерастяжимой нити, переброшенной через блок В, приводит в движение каток С, который катится без проскальзывания по наклонной плоскости (рис. 1.14). Каток и блок – однородные сплошные диски одинакового веса Q и радиуса r. Наклонная плоскость образует с горизонтом угол a. Следует составить дифференциальное уравнение движения системы под действием сил тяжести и затем определить из полученного уравнения ускорение груза А. За обобщенную координату рекомендуется взять xA.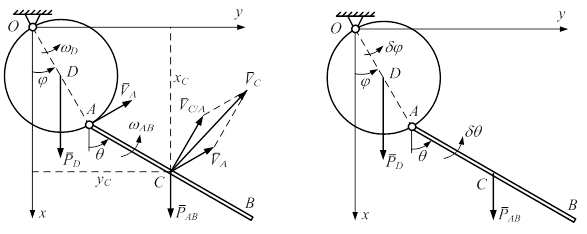
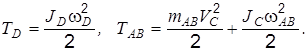
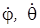 :
: 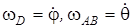 ; скорость точки C найдем по формуле
; скорость точки C найдем по формуле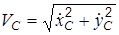 ,
, ,
,  ; дифференцируя эти координаты по времени и подставляя результаты в формулу для VC, получим
; дифференцируя эти координаты по времени и подставляя результаты в формулу для VC, получим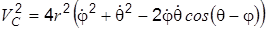 .
.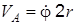 ) и скорости от вращения точки С вокруг полюса А (
) и скорости от вращения точки С вокруг полюса А (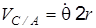 ). Построение параллелограмма выполнено на рис. 1.15.
). Построение параллелограмма выполнено на рис. 1.15.
 .
.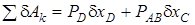 .
.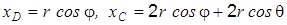 .
. . (л)
. (л)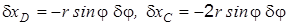 ;
;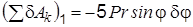 ,
,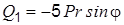 .
.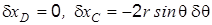 ;
; ,
, .
.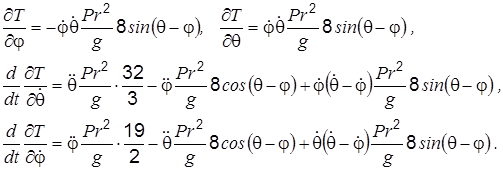

 Задача 1.4. Цилиндр В (рис. 1.17) весом Р и радиусом r, скатываясь по наклонной плоскости призмы А, приводит ее в движение по гладкому горизонтальному полу. Вес призмы А равен Q. Проскальзывание между цилиндром и призмой отсутствует. Цилиндр считать однородным сплошным телом. Составить дифференциальные уравнения движения данной системы под действием сил тяжести и определить из полученных уравнений ускорение призмы А и ускорение центра В цилиндра относительно призмы. В качестве обобщенных координат рекомендуется взять смещение s 1 призмы по полу и смещение s 2 центра В цилиндра по наклонной плоскости призмы.
Задача 1.4. Цилиндр В (рис. 1.17) весом Р и радиусом r, скатываясь по наклонной плоскости призмы А, приводит ее в движение по гладкому горизонтальному полу. Вес призмы А равен Q. Проскальзывание между цилиндром и призмой отсутствует. Цилиндр считать однородным сплошным телом. Составить дифференциальные уравнения движения данной системы под действием сил тяжести и определить из полученных уравнений ускорение призмы А и ускорение центра В цилиндра относительно призмы. В качестве обобщенных координат рекомендуется взять смещение s 1 призмы по полу и смещение s 2 центра В цилиндра по наклонной плоскости призмы. . Пренебрегая массами блока D, нити и пружины, а также сопротивлением движению, определить уравнения движения грузов. В начальный момент грузы неподвижны
. Пренебрегая массами блока D, нити и пружины, а также сопротивлением движению, определить уравнения движения грузов. В начальный момент грузы неподвижны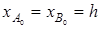 , s 0 =
, s 0 = 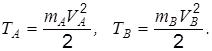
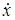 и
и 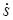 .
.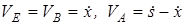 .
.
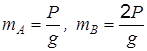 ,
, .
.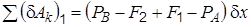 ,
,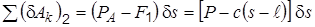 ,
, .
.
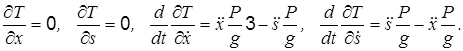
 .
.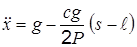 , (м)
, (м)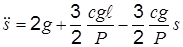 . (н)
. (н) , (п)
, (п)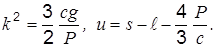
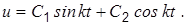
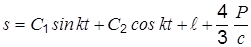 . (р)
. (р)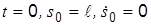 найдем
найдем
 . (с)
. (с) .
.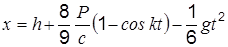 .
.