Принцип Даламбера для материальной точки и механической системы
Рассмотрим движение для несвободной точки и запишем для неё второй закон Ньютона:
Для материальной точки, векторная сумма активной силы F, реакций связи R и силы инерции Даламбера Замечание: значение принципа Даламбера в том, что уравнение динамики можно представить в виде уравнения статики.
Принцип возможных перемещений. Число степеней свободы. Пусть материальная система находится в равновесии. Силы, действующие на каждую ее точку, уравновешиваются. Если
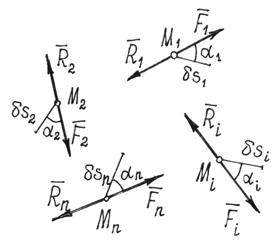
Рис.65
Дадим системе какое-нибудь возможное перемещение. Все точки ее получат перемещения Затем вычислим работу всех сил на этих перемещениях. Так как силы, приложенные к каждой точке уравновешиваются и
Если связи идеальные, то вторая сумма всегда равна нулю. Значит,
Этот результат, уравнение работ, называют общим уравнением статики. При равновесии материальной системы с идеальными и стационарными связями сумма работ всех активных, задаваемых, сил на любом возможном перемещении системы из положения равновесия равна нулю. Для определения числа степеней свободы системы поступают следующим образом. Вначале у системы исключают одну степень свободы (для этого закрепляют точку, движущуюся по заданной линии, или закрепляют вращающееся тело). Если после этого подвижность системы будет полностью устранена, значит, у системы одна степень свободы. Если же подвижность сохранится, то исключают еще одну степень свободы; и так далее до полного устранения подвижности системы (до полной остановки системы). Число таких исключений равно числу степеней свободы системы.
|


 в каждый момент времени равно нулю.
в каждый момент времени равно нулю. – равнодействующая всех активных сил, приложенных к i -той точке, а
– равнодействующая всех активных сил, приложенных к i -той точке, а  – реакция связей этой точки, то (рис.65)
– реакция связей этой точки, то (рис.65)
 ,
,  ,
,  , …,
, …,  .
. , то сумма работ этих сил на перемещении
, то сумма работ этих сил на перемещении  будет равна нулю:
будет равна нулю: 
 . Значит и сумма работ всех сил, приложенных ко всем точкам, будет равна нулю
. Значит и сумма работ всех сил, приложенных ко всем точкам, будет равна нулю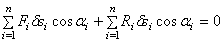 .
. (1)
(1)


