Общие указания
Уравнения Лагранжа второго рода (далее – уравнения Лагранжа) представляют собой дифференциальные уравнения движения системы в обобщенных координатах [1]. Обобщенные координаты – независимые между собою переменные параметры системы, однозначно определяющие положение системы в любой момент времени. Число обобщенных координат системы с голономными связями*) (ниже рассматриваются только такие системы) равно числу ее степеней свободы. Уравнения Лагранжа имеют вид
где n – число степеней свободы голономной системы, qi – обобщенные координаты, Кинетическую энергию системы со стационарными связями**) (ниже рассматриваются системы именно с такими связями) целесообразно до подстановки в уравнения (1.1) представить в виде функций обобщенных координат и обобщенных скоростей
Чтобы из уравнений Лагранжа (1.1) получить дифференциальные уравнения движения системы, нужно уметь: · устанавливать число степеней свободы системы (подразд. 1.2), · выбирать ее обобщенные координаты (подразд. 1.3), · определять обобщенные силы (подразд. 1.4), · составлять выражение кинетической энергии системы в обобщенных координатах (подразд. 1.5). Выполнение этих операций будем рассматривать на следующих трех примерах.
|

 , i = 1, 2, …, n, (1.1)
, i = 1, 2, …, n, (1.1) – обобщенные скорости (производные обобщенных координат по времени t), Qi – обобщенные силы, T – кинетическая энергия системы,
– обобщенные скорости (производные обобщенных координат по времени t), Qi – обобщенные силы, T – кинетическая энергия системы,  и
и 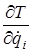 – частные производные кинетической энергии системы по обобщенной координате qi и по обобщенной скорости
– частные производные кинетической энергии системы по обобщенной координате qi и по обобщенной скорости  ,
,  – производная
– производная  . (1.2)
. (1.2)


