Выбор обобщенных координат
Напомним, что обобщенными координатами называются независимые между собой переменные параметры системы, которые однозначно определяют положение тел и точек этой системы в любой момент времени. В качестве обобщенных координат обычно выбирают углы поворота тел системы или координаты ее точек. Начало и положительное направление отсчета каждой обобщенной координаты рекомендуется выбирать так, чтобы в процессе движения эти координаты возрастали. Если система имеет положение статического равновесия, то начало отсчета рекомендуется выбирать так, чтобы в положении статического равновесия все обобщенные координаты системы были равны нулю. Во многих случаях выбор обобщенных координат определяется условием задачи. Если в задаче нужно найти ускорение а некоторой точки, движущейся вдоль оси x, то в качестве обобщенной координаты следует взять координату x этой точки, то есть q = x. Тогда искомое ускорение
Пример 1.1 (рис. 1.1) В качестве обобщенной координаты системы можно выбрать координату s точки A, отсчитываемую вдоль линии ее движения от какой-либо неподвижной точки на этой линии в направлении движения точки A. Если бы по условию задачи требовалось определить угловое ускорение барабана B, то в качестве обобщенной координаты системы следовало взять угол j поворота барабана, отсчитываемый от какого-либо начала отсчета в направлении вращения барабана.
Пример 1.2 (рис. 1.2) Предполагая, что точки A и D движутся вниз, в качестве обобщенных координат системы следует взять xA и xD, отсчитываемые от оси y вниз. Если в результате решения задачи окажется, что
Пример 1.3 (рис. 1.3) Эта система имеет положение статического равновесия, в котором стержень AB совпадает с осью x, а сила тяжести G шарика D уравновешена силой упругости пружины. Напомним, что сила упругости пружины F = G + cs. (а)
В качестве обобщенных координат системы в данном примере следует взять угол j поворота стержня AB и расстояние s шарика D от его положения, в котором деформация пружины равна l.
|

 . Если же в задаче требуется найти угловое ускорение e тела, вращающегося вокруг оси, то в качестве обобщенной координаты следует взять угол j поворота тела вокруг этой оси. Тогда искомое угловое ускорение
. Если же в задаче требуется найти угловое ускорение e тела, вращающегося вокруг оси, то в качестве обобщенной координаты следует взять угол j поворота тела вокруг этой оси. Тогда искомое угловое ускорение 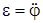 .
. (или
(или  ), то это будет означать, что точка A (или D) движется вверх.
), то это будет означать, что точка A (или D) движется вверх.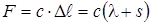 , где c – коэффициент жесткости пружины,
, где c – коэффициент жесткости пружины,  – ее деформация в произвольном положении шарика D; l – деформация пружины в положении статического равновесия системы. Учитывая, что l = G / c, получим
– ее деформация в произвольном положении шарика D; l – деформация пружины в положении статического равновесия системы. Учитывая, что l = G / c, получим


