Обобщенная сила системы с одной степенью свободы
Для системы с одной степенью свободы обобщенной силой, соответствующей обобщенной координате q, называют величину, определяемую формулой
где d q – малое приращение обобщенной координаты; Напомним, что возможное перемещение системы определяется как перемещение системы в бесконечно близкое положение, допускаемое связями в данный момент времени (подробнее см. прил. 1). Известно, что сумма работ сил реакций идеальных связей на любом возможном перемещении системы равна нулю. Поэтому для системы с идеальными связями в выражении
d А(
а в координатной форме – выражение
d А(
Если пара сил с моментом М приложена к вращающемуся телу, угловая координата которого есть j, а возможное перемещение dj, то элементарная работа момента М на возможном перемещении dj определяется по формуле d А(М) = ± M d j. (1.3в)
Здесь знак (+) соответствует случаю, когда момент М и возможное перемещение dj совпадают по направлению; знак (–), когда они противоположны по направлению. Чтобы можно было по формуле (1.3) определить обобщенную силу, надо возможные перемещения тел и точек в Определение обобщенной силы Q, соответствующей выбранной обобщенной координате q, рекомендуется производить в следующем порядке. · Изобразить на расчетной схеме все активные силы системы. · Дать малое приращение обобщенной координате d q > 0; показать на расчетной схеме соответствующие возможные перемещения всех точек, в которых приложены силы, и возможные угловые перемещения всех тел, к которым приложены моменты пар сил. · Составить выражение элементарной работы · Определить обобщенную силу по формуле (1.3). Пример 1.4 (см. условие к рис. 1.1). Определим обобщенную силу, соответствующую обобщенной координате s (рис. 1.4). На систему действуют активные силы: P – вес груза; G – вес барабана и вращающий момент M. Шероховатая наклонная плоскость является для груза А неидеальной связью. Сила трения скольжения Fтр, действующая на груз A со стороны этой связи, равна Fтр = f N. Для определения силы N нормального давления груза на плоскость при движении воспользуемся принципом Даламбера: если к каждой точке системы помимо действующих активных сил и сил реакций связей приложить условную силу инерции, то образованная совокупность сил будет уравновешенной и уравнениям динамики можно придать форму уравнений равновесия статики [1]. Следуя известной методике применения этого принципа [3], изобразим все силы, действующие на груз A (рис. 1.5), –
Рис. 1.4 Рис. 1.5
Добавим силу инерции Отсюда N = P cos a. Силу трения скольжения теперь можно определить по формуле Fтр = f P cos a.
Дадим обобщенной координате s малое приращение d s > 0. При этом груз (рис. 1.4) переместится вверх по наклонной плоскости на расстояние d s, а барабан повернется против часовой стрелки на угол dj. Составим по формулам типа (1.3а) и (1.3в) выражение суммы элементарных работ момента M, сил P и Fтр:
выразим в этом уравнении dj через d s:
определим обобщенную силу по формуле (1.3)
учтем записанную ранее формулу для Fтр и получим окончательно
Если в этом же примере за обобщенную координату взять угол j, то обобщенная сила Qj выразится формулой
Рекомендуется самостоятельно проверить достоверность этого результата.
1.4.2. Определение обобщенных сил системы Если система имеет n степеней свободы, ее положение определяют n обобщенных координат. Каждой координате qi (i = 1, 2, …, n) соответствует своя обобщенная сила Qi, которая определяется по формуле
где При определении Обобщенные силы системы с двумя степенями свободы рекомендуется определять в следующем порядке. · Показать на расчетной схеме все активные силы системы. · Определить первую обобщенную силу Q1. Для этого дать системе первое возможное перемещение, когда d q1 > 0, а d q2 = 0; показать на расчетной схеме соответствующие d q1 возможные перемещения всех тел и точек системы; составить · Определить вторую обобщенную силу Q2. Для этого дать системе второе возможное перемещение, когда d q2 > 0, а d q1 = 0; показать на расчетной схеме соответствующие d q2 возможные перемещения всех тел и точек системы; составить
Пример 1.5 (см. условие к рис. 1.2) Определим Q1 и Q2, соответствующие обобщенным координатам xD и xA (рис. 1.6, а). На систему действуют три активные силы: PA = 2P, PB = PD =P.
Рис. 1.6
Определение Q1. Дадим системе первое возможное перемещение, когда d xD > 0, d xA = 0 (рис. 1.6, а). При этом груз D переместится по вертикали вниз на расстояние d xD, блок B повернется против часовой стрелки на угол dj B, ось цилиндра A останется неподвижной, цилиндр A повернется вокруг оси A на угол dj A по часовой стрелке. Составим сумму работ на указанных перемещениях:
определим
Определим Q2. Дадим системе второе возможное перемещение, когда d xD = 0, d xA > 0 (рис. 1.6, б). При этом ось цилиндра A переместится по вертикали вниз на расстояние d xA, цилиндр A повернется вокруг оси A по часовой стрелке на угол dj A, блок B и груз D останутся неподвижными. Составим сумму работ на указанных перемещениях:
определим
Пример 1.6 (см. условие к рис. 1.3) Определим Q1 и Q2, соответствующие обобщенным координатам j, s (рис. 1.7, а). На систему действуют четыре активные силы: вес стержня P, вес шарика
Рис. 1.7
Учтем, что Отметим, что точка приложения силы F2 неподвижна, поэтому работа этой силы на любом возможном перемещении системы равна нулю, в выражение обобщенных сил сила F2 не войдет. Определение Q1. Дадим системе первое возможное перемещение, когда dj > 0, d s = 0 (рис. 1.7, а). При этом стержень AB повернется вокруг оси z против часовой стрелки на угол dj, возможные перемещения шарика D и центра E стержня направлены перпендикулярно отрезку AD, длина пружины не изменится. Составим
(Обратим внимание на то, что Выразим перемещения d xE и d xD через dj. Для этого вначале запишем
Затем в соответствии с формулой (7) прил. 1 найдем
Подставляя найденные величины в
По формуле (1.4), учитывая, что
Определение Q2. Дадим системе второе возможное перемещение, когда dj = 0, d s > 0 (рис. 1.7, б). При этом стержень AB останется неподвижным, а шарик M сместится вдоль стержня на расстояние d s. Составим сумму работ на указанных перемещениях:
определим
подставив значение силы F1 из формулы (а), получим
1.5. Выражение кинетической энергии системы Кинетическая энергия системы равна сумме кинетических энергий ее тел и точек (прил. 2). Чтобы получить для T выражение (1.2), следует скорости всех тел и точек системы выразить через обобщенные скорости, используя методы кинематики [2]. При этом система считается находящейся в произвольном положении, все ее обобщенные скорости считаются положительными, т. е. направленными в сторону возрастания обобщенных координат.
Пример 1. 7 (см. условие к рис. 1.1)
T = TA + TB.
По формулам (2) и (3) прил. 2 имеем: Далее выразим VA и w B через Подставляя эти данные в T и учитывая, что
Пример 1.8 (см. условие к рис. 1.2)
T = TA + TB + TD. По формулам (2), (3), (4) прил. 2 запишем
Выразим VA, VD, wB и w A через
При определении w A учтено, что точка O (рис. 1.9) – мгновенный центр скоростей цилиндра A и Vk = VD (см. соответствующие пояснения к примеру 2 прил. 2). Подставляя полученные результаты в T и учитывая, что
определим
Определим кинетическую энергию системы на рис. 1.10, взяв в качестве обобщенных координат j и s, T = TAB + TD. По формулам (1) и (3) прил. 2 имеем
Выразим w AB и VD через
где
Подставляя эти результаты в T и учитывая, что
получим
1.6. Составление дифференциальных уравнений Чтобы получить искомые уравнения, нужно в уравнения Лагранжа (1.1) подставить найденное ранее выражение кинетической энергии системы в обобщенных координатах и обобщенные силы Q 1, Q 2, …, Qn. При нахождении частных производных T по обобщенным координатам При выполнении операции Подчеркнем, что уравнения Лагранжа
|

 , (1.3)
, (1.3)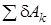 – сумма элементарных работ сил системы на ее возможном перемещении.
– сумма элементарных работ сил системы на ее возможном перемещении. (Fkx, Fky, Fkz) приложена в точке К, радиус-вектор которой есть
(Fkx, Fky, Fkz) приложена в точке К, радиус-вектор которой есть  (xk, yk, zk), а возможное перемещение –
(xk, yk, zk), а возможное перемещение –  (d xk, d yk, d zk). Элементарная работа силы
(d xk, d yk, d zk). Элементарная работа силы  , которому в аналитической форме соответствует выражение
, которому в аналитической форме соответствует выражение ), (1.3а)
), (1.3а) и
и  , где
, где 
 , где
, где  – ускорение груза. Уравнение принципа Даламбера в проекции на ось y имеет вид N – P cos a = 0.
– ускорение груза. Уравнение принципа Даламбера в проекции на ось y имеет вид N – P cos a = 0. ;
; , тогда
, тогда ;
; ,
,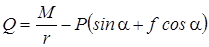 . (б)
. (б) .
. , (1.4)
, (1.4)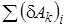 – сумма элементарных работ активных сил на i -м возможном перемещении системы, когда d qi > 0, а остальные обобщенные координаты неизменны.
– сумма элементарных работ активных сил на i -м возможном перемещении системы, когда d qi > 0, а остальные обобщенные координаты неизменны. – выражение элементарной работы сил системы на первом возможном перемещении; возможные перемещения в
– выражение элементарной работы сил системы на первом возможном перемещении; возможные перемещения в  – выражение элементарной работы сил системы на втором возможном перемещении; возможные перемещения в
– выражение элементарной работы сил системы на втором возможном перемещении; возможные перемещения в 
 ;
;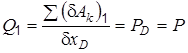 . (в)
. (в) ;
;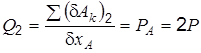 . (г)
. (г) , силы упругости пружины
, силы упругости пружины 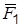 и
и  .
.
 . Модуль сил упругости определяется по формуле (а).
. Модуль сил упругости определяется по формуле (а). .
. , поэтому работа этой силы на первом возможном перемещении равна нулю).
, поэтому работа этой силы на первом возможном перемещении равна нулю). ,
, 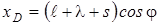 .
. ,
, 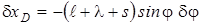 .
. .
. , определим
, определим . (д)
. (д)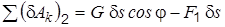 ;
; ;
; . (е)
. (е) Определим кинетическую энергию системы (рис. 1.8), взяв в качестве обобщенной координаты расстояние s,
Определим кинетическую энергию системы (рис. 1.8), взяв в качестве обобщенной координаты расстояние s, .
.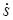 :
:  .
. , получим
, получим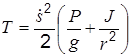 . (ж)
. (ж) Определим кинетическую энергию системы на рис. 1.9, взяв в качестве обобщенных координат величины xD и xA,
Определим кинетическую энергию системы на рис. 1.9, взяв в качестве обобщенных координат величины xD и xA,
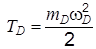 .
. :
: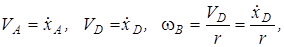
 .
. ,
, . (и)
. (и) Пример 1.9 (см. условие к рис. 1.3)
Пример 1.9 (см. условие к рис. 1.3)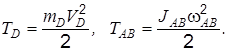
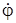 и
и 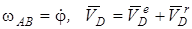 ,
,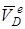 – переносная скорость шарика D, ее модуль определяется формулой
– переносная скорость шарика D, ее модуль определяется формулой ,
, – относительная скорость шарика, ее модуль определяется по формуле
– относительная скорость шарика, ее модуль определяется по формуле  ,
,  .
. ,
,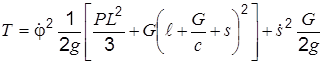 . (к)
. (к) и по обобщенным скоростям
и по обобщенным скоростям 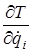 следует учитывать, что переменные q 1, q 2, …, qn;
следует учитывать, что переменные q 1, q 2, …, qn;  считаются независимыми между собой. Это значит, что определяя частную производную T по одной из этих переменных, все остальные переменные в выражении для Т следует рассматривать как постоянные величины.
считаются независимыми между собой. Это значит, что определяя частную производную T по одной из этих переменных, все остальные переменные в выражении для Т следует рассматривать как постоянные величины. следует дифференцировать по времени все входящие в
следует дифференцировать по времени все входящие в  записываются для каждой обобщенной координаты qi (i = 1, 2, …n) системы.
записываются для каждой обобщенной координаты qi (i = 1, 2, …n) системы.


