ГЛАВА 2. ОТОЖДЕСТВЛЕНИЕ ОБЪЕКТА НАБЛЮДЕНИЙ С СИСТЕМОЙ
Идентификация объекта связана с абстракцией отождествления. Идентификация - это " установление соответствия распознаваемого объекта своему образу (знаку)" [32]. Имя предмета, множество описаний его свойств и отношений, выделение существенных признаков для определения классов понятий и отношений являются средствами " групповой идентификации" объекта наблюдений в среде и между объектами, т.е. являются средствами базирования в смысле {(Вj; bj)}. Для идентификации и группового базирования применяются рациональные системы описаний на уровнях У1; У2; У3; У4. Французское слово " база" и греческое " базис" означают основу чего-либо, основание, фундамент, в данном случае основа для идентификации объекта наблюдения среди множества других. От базы, как от основания, можно строить систему описаний и моделей объекта наблюдений. В качестве базиса (базы) используются три понятия: · групповое описание, идентифицирующие объект наблюдений, как предмет, вещь, событие, мероприятие, исследуемую операцию (Г; G); · пространственное описание объекта в среде по отношению к другим объектам и процессам, (П или Р); · временное или время-подобное описание поведения объекта в пространстве наблюдений, в пространстве состояний и переходов (В; Т). Рассмотрим уровни описания объекта для его группового базирования, т.е. отождествления объекта, как части мира, выделенной субъектом для наблюдений. 2.1. СИСТЕМА НА ЗНАКОВО-ЛИНГВИСТИЧЕСКОМ УРОВНЕ - У1 На лингвистическом уровне имена предметов называют термами. Отношения между термами описываются с помощью функторов. Итак, множество понятий, связанных с объектом наблюдений, разбиваются на два типа подмножеств: на термы и функторы. Знания субъекта об объекте наблюдений формируются в виде множества правильных высказываний. Сами термы и функторы также определяются как правильные высказывания. Под правильным высказыванием понимается утвердительная форма предложения, истинность или ложность которого определена субъектом логически или операционно (по каналу наблюдений или каналу абстрагирования). При описании объекта на уровне У1 некоторые термы могут варьироваться субъектом, т.е. определяются как константы, задаваемые субъектом в процессе конкретизации наблюдений. Подобные термы в общем случае называются конституэнтами. В качестве конституэнт выступают, в частности, физические константы, коэффициенты уравнений, параметры среды наблюдений и т.п. Из термов, конституэнт и функторов строят предложения (высказывания), которые могут быть истинными при определенных значениях конституэнт. В общем случае множество высказываний образует систему правильных высказываний (П), часть из которых истинная (Т). Если конституэнты в Т-высказываниях являются формально определяемыми величинами, то множество правильных высказываний Т на множестве П образует теорию. На лингвистическом уровне (по Месаровичу) система (å 1) определяется как множество правильных высказываний, построенных из термов и функторов: [29] S Û å 1=(A; R)=({термы, конституэнты}; {функторы}). Задачи и упражнения 1. Для работ, проводимых в огороде в мае месяце для картофеля, в таблице Жукова находим следующую систему высказываний. " В мае продолжают проращивать до посадки поздний картофель. С 1 по 5 мая сажают рассаду раннего картофеля под пленку (на случай заморозков). При температуре почвы +(8-10 С°) сажают клубни по схеме 60´ ЗО´ 6 см; при посадке опыляют золой. 15-25 мая сажают поздние сорта. При росте кустиков в 20 см окучивают, предварительно удобряя и увлажняя почву". а. Является ли данное множество высказываний правильным в общем случае и по Месаровичу? б. Выделите термы, конституэнты и функторы. Определите арность отношений, описываемых функторами. в. Выделите признаки (свойства), как унарные отношения, определяемые прилагательными. г. Конкретизируйте понятия: объект, субъект, система объекта на данном примере. 2. Базовыми понятиями теории систем являются: объект, субъект, системный подход, система, задача субъекта, модель, системный анализ. …. Известны определения данных понятий по первоисточникам. а. Исследуйте по первоисточникам одно из этих понятий как систему, описываемую с помощью термов и функторов: учтите, что термами и функторами при описании каждого понятия выступают другие понятия. б. Определите множество истинных высказываний для указанной совокупности понятий, которое можно принять в качестве основы теории систем (на лингвистическом уровне). в. Предложите описание отношений понятий в данной теории в виде графа: Г(Х; У), где X - вершина графа (понятия); У - ребра графа (отношения между понятиями), петли - унарные свойства понятий. 3. Определите отличительные признаки понятий: теория, интуитивная теория, аксиоматическая теория, дополнив систему правильных высказываний о формальных теориях и математических структурах [65]. 4. Теория матричных игр строится на таких понятиях как конфликтная ситуация, игроки, стратегия, пространство стратегий, ход, выбор, исход, выигрыши, потери, партия игры, функция потерь, правила игры [20; 24]. Постройте систему для описания матричных игр на лингвистическом уровне, т.е. как множество правильных высказываний, используя первоисточники, например [20]. 5. Имитационное моделирование трехканальной системы массового обслуживания в учебном пособии [21] рассмотрено на конкретной системе типа G/G/3/3. Составьте описание этой конкретной системы на лингвистическом уровне в виде исходного множества правильных высказываний, определяющих поведение объекта в среде наблюдений. 2.2. ТЕОРЕТИКО-МНОЖЕСТВЕННЫЙ УРОВЕНЬ Система как множество правильных высказываний X может быть представлена в виде разбиения исходных множеств на подмножества: X = Каждое подмножество Xi также представляет собой систему элементов хi Î Хi со своими свойствами и отношениями. Из множества систем можно сформировать в общем случае систему Хs, как собственное подмножество указанных множеств: Ms Í M=Х1 ´ X2 ´ …Хn={(X)}, (2.1) где Х = (х1, х2,... хn); X - кортеж, вектор, последовательность (в зависимости от свойств объекта). Объект X может быть точкой в n-мерном пространстве (математический объект) или описанием конкретного объекта по множеству признаков (быть базой для идентификации объекта). Итак, система на уровне абстрагирования У2 представляет собой собственное подмножество (МS) множества М, определенного на прямом произведении множеств Х1; Х2; …Хn. При этом решается задача распознавания и классификации термов на уровне множеств. Функторы определяются в отношениях на множествах. Вводится соответствующая система обозначений множеств и их элементов. Задачи и упражнения 1. Определите на примере таблицы Жукова (см. упр. п.2.1) базовые множества вида Х1 ´ Х2 и возможные подмножества Хs Ì X1 ´ Х2. В чем проявляется сходство описаний таблицы Жукова и индикатора символов с числом ячеек m ´ n?. 2. Известно определение множества по Н. Бурбаки: " Множество образуется из элементов, обладающих некоторыми свойствами и находящимися в некоторых отношениях между собой или с элементами других множеств". Пусть объект представляет собой индикатор для визуализации множества символов размера 7 ´ 5. Подобные индикаторы применяются в различных реальных устройствах. Множество элементов индикатора равно 35 и упорядочено в пространстве 5 ´ 7, как показано на рисунке. Х2

а. Опишите работу одного из этих устройств в виде системы правильных высказываний. б. Определите свойства элементов для выделенных на индикаторе трех множеств Х1 = {1; …7}; Х2 = {1;...5}; Х3={1;...35}. в. Приведите содержательное описание систем типа г. Понятие " множество" (по Бурбаки) является системой. Проиллюстрируйте это с помощью понятия " граф". Для этого термы определите как вершины графа, а функторы - как петли, ребра или дуги графа. 3. Дано Х = Х1 ´ X2 ´ …Хn = {(х1; х2;...хn)}, ПрiX; ПрjХ; Прi, l, kХ, здесь Пр - проекция. 2.3. АБСТРАКТНО - АЛГЕБРАИЧЕСКИЙ УРОВЕНЬ Этот уровень абстрагирования - конкретизации связан с математическими объектами типа: Г: М1 ´ М2 ´...Мn ® Мn+1; М Ì N, где Г- обозначение математической структуры и алгебраической операции (в зависимости от смыслового оттенка утверждения); {М}- базовые множества Г структуры (носители структуры); {´; ®}- обозначение системы отношений, определенной на базовых множествах (произведение множеств и следование); N - упорядоченное множество элементов, например, множество натуральных чисел, кортеж событий, алфавит символов.... Конкретизируя систему свойств и отношений, например, в виде наборов постулатов (системы аксиом) получим, в частности, абстрактно-алгебраические структуры типов: группоида, полугруппы, группы, кольца, модуля, тела, поля, решетки...., которые определяют целые классы формальных систем вида: S = (M1; M2;; p1; p2;; a1; a2); здесь: S - алгебраическая система (математическая структура); {М}- базовые множества определения системы; {р}- отношения, определенные на элементах множества; {a}- свойства, образующие систему аксиом К(a) или систему истинных утверждений (теорию в смысле лингвистического подхода). Система отношений {р} может определяться на множествах: R1; R2; R3;...Rn типов отношений, где индекс обозначает " арность" или " местность" отношения: R1 - множество унарных /одноместных отношений; R2 - множество бинарных /двухместных отношений; … Rn - множество энарных /энместных отношений. С помощью R1, в частности, описывается общее свойство элементов из данного множества-универсума по выделенному свойству. Примерами бинарных отношений являются композиции, соответствия, отношения, отображения, в которых паре элементов ставится в соответствие третий элемент [2]. Функции (функционалы, операторы) являются классами объектов, определяемых на различных уровнях отношений: У = f(x) или f(x, У) = 0 - двухместное отношение; z = f(x, У) или f(x, У, z) = 0 - трехместное отношение; q = f(x, У, z) или f(x, У, z, q) = 0 - четырехместное отношение. Схема представления функции имеет вид направленной или ненаправленной кибернетической системы:
Итак, понятие системы на абстрактно-алгебраическом уровне конкретизируется с учетом уровней У1 и У2. На уровне У1 определяется теория, как множество правильных высказываний о свойствах объекта исследований {a}. На уровне У2 конкретизируется множество элементов и их отношений {М}. Множество подмножеств {М} выбирается в качестве базы. На уровне УЗ конкретизируется понятие алгебраической операции в виде системы отношений {р}. Задачи и упражнения 1. Свойствами математических объектов, в частности, являются: рефлексивность (1), антирефлексивность (2), симметричность (3), антисимметричность (4), несимметричность (5), транзитивность (6): Проиллюстрируйте указанные свойства в виде систем отношений на графах и на матрицах для множества из 4-х элементов {а, b, с, d}. 2. Известны системы отношений: эквивалентность (1), предпорядок (2), порядок нестрогий (3), строгий порядок (4), толерантность (5), доминирование (6). а. Составьте таблицу свойств для этих отношений в виде алгебраической абстракции операций вида Х ´ Y ® А и Y ´ X ® В б. Сравните свойства таблиц А и В. в. Определите модели систем, представляющие указанные отношения на графах и матрицах. 3. В понятиях групповых структур одинакового порядка изоморфизм определяется наличием двух свойств одновременно: инъекции и сюръекции. Говорят в этом случае о биективном (двойном) отображении. Гомоморфизм имеет место при наблюдении одного из указанных свойств и разделяется на мономорфизм (при инъекции) или эпиморфизм (при сюръекции). Определите изоморфизм понятий и схему соответствий для физических и математических систем, описываемых уравнениями: L ma + kv + ws = F - механическая система;
Определите понятие модели на основе свойства изоморфизма. 4. Для групповых операций мультипликативности и аддитивности на множестве {а, b, с} запишите алгебраические законы: сочетательный (ассоциативный), переместительный (коммутативный) и распределительный (дистрибутивный). Определите понятия нейтрального и обратного (противоположного) элементов. 5. Алгебраическая система задана таблицей: Х ´ У ® У1
Здесь Х = У = У1 = {0, 1, 2,...6}. Мощность множеств равна:
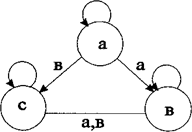
Таблицу можно рассматривать как одно из возможных высказываний. Какова мощность источника высказываний для системы аргументов X и У? 6. Определите классы отношений и их интерпретацию для системы знаков: {=; º; ~; «; ½ ½; ^; <; £; ³; >; Î; Í; È; Ç; ¤; Þ; Û }. Дополните систему знаков известными Вам и выделите неизвестные. 7. Алгебраическая система типа Т: А ´ А ® А называется композицией объектов. Композиция может быть представлена таблицей или графом композиции, например:
Постройте граф композиции для следующего комплекса систем Т:
К какому классу алгебраических систем относятся системы
|

 Æ;
Æ;

 + Ri = V- электрическая система;
+ Ri = V- электрическая система; = f(x) - математическая система.
= f(x) - математическая система.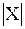 =
=  = 6
= 6