ЛОГИКО-МАТЕМАТИЧЕСКИЙ УРОВЕНЬ ОПИСАНИЯ СИСТЕМ - У4
Логико-математическая интерпретация алгебраического уровня описания достигается путем идентификации значений истинности и ложности и их модальностей на отрезке [0, 1], как универсуме. Для положительной двухзначной логики без модальностей - это крайние точки отрезка: 0 - ложно, 1- истинно. При этом значения аргументов и функции определяются на одном и том же множестве {0, 1}.
Логическая операция в общем случае записывается, как частный случай алгебраической: j: где k - значность логики, определяется мощностью NK. Для двузначной логики N2 = {0; 1}, т.е. мощность множества Логическая интерпретация определяет систему отношений элементов множества Nk к областям истинности и ложности. Кроме положительной, различают отрицательную и смешанные типы логик. Если ввести десятичный эквивалент двоичных наборов и использовать его для упорядоченного описания номеров наборов аргументов и номеров функций, то алгебраической базой описания логического пространства являются алгебраические выражения вида: j: где n - число аргументов; Nn - число наборов аргументов; Nm - число логических функций. Для двухзначной логики имеем: Nn Î {0, 2, 4, 8, … q}; q = 2n; Nm = {0, 2, 4, 8, 16, 32..., r}; r = 2q. Для k - значной логики q = kn и r = kq. Таким образом, формально между допустимыми множествами значений Nn и Nm для двухзначной логики имеется степенная зависимость вида
Для идентификации функций при n = 4 по десятичным номерам удобно использовать модель логического пространства в виде карты Карно:
Теоретико-множественные и алгебраические операции при описании функции на логико-математическом уровне конкретизируются в наборе логических операций: R Û {┐; Ù; Ú; ┐ Ú; ¯; ┐ Ù; /; ®; «; Å... }. Задачи и упражнения 1. Составьте алгебраические системы для следующих логических операций: отрицание(┐), дизъюнкция(Ú), конъюнкция(Ù), импликация(®), эквиваленция(º). Как называются подобные таблицы в математической логике? 2. Для одной из ячеек системы высказываний таблицы Жукова, определяющей краткий план работ в саду и огороде, постройте логические формулы, введя соответствующую систему обозначений для множества правильных высказываний. Сколько ячеек может содержать таблица Жукова? Введите для таблицы Жукова понятие " алгебраическая структура и операция". 3. Номер логической функции задан десятичным числом k из множества {0,.....65531}. Задайтесь числом k. Определите соответствующую этому числу логическую функцию. Воспользуйтесь картой Карно. 4. Составьте таблицу отношений N ® N, N2 ® N при N = {0; 1} опр и N2 Û N * N. Покажите, что логическая интерпретация определяет множество булевых функций от одной или 2-х переменных соответственно. 5. Определите изоморфизм диаграмм Эйлера, Венна, кубического графа на примере одной из логических функций. 6. Полные наборы функций определяют изоморфные формы их описания. Покажите изоморфизм логических систем на примерах наборов функций Пирса - Вебба (стрелка Пирса) и функции Шеффера (штрих Шеффера). 7. Определите системное свойство следующих наборов логических функций: {константа 0, отрицание, конъюнкция, дизъюнкция}; {отрицание, конъюнкция}; {отрицание, дизъюнкция}; {стрелка Пирса}; {штрих Шеффера}. 8. Определите систему соответствий логических операций, производимых на уровне множеств (У2), и на уровне моделей математической логики (У4). 9. Известны 11 элементарных логических функций, определяемых логической формулой и кортежами свойств: (a1; a2; a3; a4; a5); 0(a2; a3); 1(a1; a3); Дайте лингвистическое определение понятий, записанных выше. Составьте соответствующую описанию таблицу в виде алгебраической операции. ГЛАВА 3. ТОПОЛОГИЯ И ТОПОЛОГИЧЕСКИЕ Всеобщие формы существования материи определяются понятиями пространства и времени. Основные свойства материи являются общесистемными: материя несотворима, неуничтожима, вечна и бесконечна. На уровне описания объекта системой высказываний, правильность которых проверяется историческим опытом людей, материя наделяется следующими свойствами: 1. Это философская категория для обозначения объективной реальности. 2. Основа (субстрат) всех реально существующих в мире свойств, связей и форм движения (всех процессов и явлений). 3. Бесконечное множество всех объектов и систем. 4. Субстанция (сущность), нечто относительно устойчивое, существующее само по себе, не зависит ни от чего другого. Итак, объект является частью материального мира, выделенного субъектом для наблюдений. Объект участвует в общем движении, расположен в пространстве и проявляет себя во времени. Движение характерно для объекта и как изменение его внутреннего состояния в пространстве параметров, так и относительно других объектов в метрических пространствах. На топологических уровнях описания пространство рассматривается в свою очередь как система, наделенная определенными математическими свойствами. Вводятся пространственно-подобные отношения: метрика объекта, расстояние между объектами и между состояниями объекта, системы координат, нормированные пространства. Объектами математических пространств являются точки, линии, плоскости, поверхности, вектора, числа и их комплексы. Итак, описание системы на топологическом уровне конкретизируется по отношениям меры, т.е. вводятся пространственно-подобные отношения.
|




 0
0
 ® Nk; Nk = {0, 1, 2, 3, …, k-1},
® Nk; Nk = {0, 1, 2, 3, …, k-1}, = 2, или из уравнения k-1=1, следовательно k=2.
= 2, или из уравнения k-1=1, следовательно k=2. ® Nm,
® Nm,
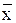 (a1; a2; a5); (x1Lx2)(a3; a4); (x1Vx2)(a3; a4);
(a1; a2; a5); (x1Lx2)(a3; a4); (x1Vx2)(a3; a4); 


