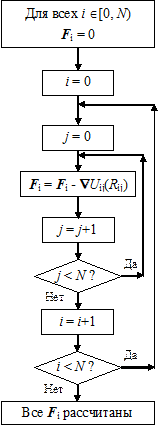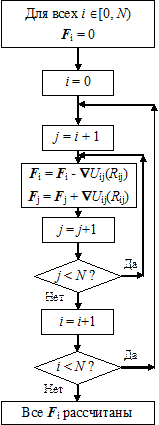Алгоритм с использованием разделяемой памяти

Самые последние графические процессоры уже поддерживают вычис­ления с двойной точностью, что в принципе позволяет полностью реализо­вывать на GPU шаги молекулярной динамики, не обращаясь к центральному процессору. Всё же, здесь мы ограничимся только рассмо­трением алгоритма расчёта межчастичных сил, который вполне демонстри­рует новые возмож­ности 4-й шейдерной модели и CUDA [69].

Этот алгоритм, приведённый на рис. 9.7, отличается от рассмотрен­ных в главе 6 тем, что включает в себя «ручную» оптимизацию использо­вания «быстрой» разделяемой параллель­ной памяти, которой не существо­вало у GPU шейдерной модели 3.0.

Кодирование алгоритма молекулярной динамики на CUDA не имеет принци­пиальных особенностей по сравнению с перемножением матриц, так что мы не будем приводить весь код. Остановимся только на одной из простых реализаций «треугольного» цикла расчёта сил, использующего 3-й закон Ньютона для двукратного уменьшения объёма вычислений.

9.5.2. Расчёт сил на GPU с использованием 3-го закона Ньютона

На рис. 9.8 a (без учёта распараллеливания) показан самый простой цикл расчёта действующих между частицами сил. На GPU SM3 можно (с распараллеливанием) реализовать только этот цикл, поскольку каждая сила F _i рассчитывается независимо от сил F _j, действующих на другие частицы. Распараллеливание этого же цикла на GPU SM4 показано на рис. 9.7.

Вместе с тем, согласно 3-му закону Ньютона, F _ij = - F _ji, то есть Ñ U _ij(R _ij) = - Ñ U _ji(R _ji). Таким образом, алгоритм расчёта сил можно модифи­цировать согласно рис. 9.8 б. В новом цикле суммирование по j начинается с j = i+ 1, а не с нуля, так что весь двойной цикл по i, j, становящийся «треугольным», содержит в 2 раза меньше операций вычисления сил. На рис. 9.9, иллюстрирующем «треугольный» цикл, тёмные прямоугольники соответствуют парам (i, j), для которых силы F _ij реально считаются, а белые – обратным комбинациям (i, j), для которых F _ji = - F _ij.

Рис. 9.7. Молекулярная динамика на графическом процессоре шейдерной модели 4.0

Ниже с комментариями приведена реализация «треугольного» цикла с 3-м законом Ньютона на CUDA. Для наглядности используется только один мультипроцессор. Каждый i -й поток суммирует парные взаимодействия i -й частицы и записывает их в разделяемую память, а в конце сохраняет одну из накопленных сумм в линейный массив force (каждой частице соответствует только один элемент), расположенный в глобальной памяти. Это позволяет минимизировать количество обращений к медленной общей памяти.

a)	б)

Рис. 9.8. Расчёт сил с учётом и без учёта 3-го закона Ньютона

Рис. 9.9. «Треугольный» цикл расчёта сил

Процедура вычисления сил в «треугольном» цикле на CUDA

/* Спецификатор __global__ означает, что вся процедура будет исполняться на GPU как вычислительное ядро */

__global__ void kernel_NxN(float4 force[], float4 pos[], int type[], float4 coefs[]) {

 

/* Переменные, описываемые без спецификаторов, будут хранится в том кэше GPU, который называют «памятью для констант». Они не будут меняться по ходу алгоритма: */

int j;

/* Вычислительные потоки в данном случае упорядочены в линейный массив. Каждый поток рассчитывает силу F _i, действующую на одну из частиц: */

int i = threadIdx.x;

/* Тип частицы type[i] и 4-вектор с координатами частицы pos[i] копируются в кэш, для того чтобы потом не обращаться за ними внутри цикла по j к медленной видеопамяти: */

int type_i = type[i];

float4 pos_i = pos[i];

/* Создаётся переменная (4-вектор) force_i, в которой будет сумми­ро­ваться результирующая сила, действующая на частицу i со стороны осталь­ных частиц; в начале расчёта она зануляется */

float4 force_i = { 0, 0, 0, 0 };

/* В разделяемой памяти (на что указывает модификатор __shared__) создаются массивы, содержащие координаты и типы всех частиц, параметры всех потенциалов взаимодействия (coefs_ij[4], где coefs_ij – сам по себе 4-вектор), а также все результирующие силы (force_j[N]), действующие на каждую из частиц: */

__shared__ float4 pos_j[N];

__shared__ int type_j[N];

__shared__ float4 coefs_ij[4];

__shared__ float4 force_j[N];

/* Следующий блок операторов копирует данные из медленной «глобальной» памяти GPU, куда их перед обращением к GPU записывает центральный процессор, в быструю разделяемую память. Каждый из потоков копирует элементы массивов, относящиеся к «своей» частице i, а первые 4 потока – ещё и параметры потенциалов взаимодействия */

if (threadIdx.x < 4) coefs_ij[i] = coefs[i];

pos_j[i] = pos[i]; type_j[i] = type[i];

force_j[j] = make_float4(0, 0, 0, 0);

/* Синхронизация потоков. Выполнение программы за функцией __syncthreads() продолжится только после того, как все потоки завершат копирование данных в разделяемую память */

__syncthreads();

/* Цикл, в котором суммируется сила, действующая на i -ю частицу со стороны остальных. Индекс j изменяется до N + i для того, чтобы во всех потоках, независимо от значения i, в этом цикле было одинаковое количество итераций. Фактически, при j ³ N внутри цикла ничего не делается */

for (j = i+1; j < N + i; j++)

{

if (j < N)

{

/* Функция force_ij возвращает силу, действующую между части­цами i и j. Аргументами функции являются координаты частиц и параметры потенциала взаимодействия */

float4 Fij = force_ij(pos_i, pos_j[j], coefs_ij[type_i + type_j[j]]);

/* Применение 3-го закона Ньютона

force_i += Fij; force_j[j] -= Fij;

}

/* Синхронизация потоков, необходимая для устранения возможных конфликтов доступа к элементам массива force_j[j]: */

__syncthreads();

}

/* Получение окончательных результирующих сил

force[i] = force_i + force_j[i];

}

 

/* Функция расчёта парной силы force_ij. Возвращает 4-вектор с компонентами силы (четвёртый элемент – пустой). Спецификатор __device__ означает, что функция и вызывается, и исполняется графическим процессором */

__device__ float4 force_ij(float4 pos_i, float4 pos_j, float4 c)

{

float4 R = pos_i - pos_j; R.w = rsqrt(max(R * R, 1e-4));

return R * (c.x * R.w * R.w * R.w + pow(c.y * R.w, c.z));

}