Работа с топографической картой
Введение Цель работы: научиться читать топографическую карту (т.е. получать правильное представление о рельефе местности, гидрографии, населенных пунктах, путях сообщения, растительном покрове, естественных и сельскохозяйственных угодьях и т.п. по их изображению в условных знаках), решать по карте (плану) конкретные инженерно-геодезические задачи. В соответствии с этим при выполнении задания студенту следует решить по карте (плану) следующие инженерно-геодезические задачи: 1. Определение горизонтальных проложений линий с помощью масштабов; 2. Определение геодезических и прямоугольных координат точек; 3. Определение истинных и магнитных азимутов и дирекционных углов направлений; 4. Решение прямой и обратной геодезических задач на координаты; 5. Определение отметок точек по горизонталям; 6. Определение уклона и крутизны ската по горизонталям; 7. Проектирование трассы с заданным уклоном; 8. Построение профиля местности по заданному направлению; 9. Определение границ водосборной площади. Выполнение работы предусматривает обязательное изучение соответствующих разделов учебной литературы: 1. А.В. Маслов, А.В. Гордеев, Ю.Г. Батраков. Геодезия: Учебник для вузов. – М.: Колос, 2006, гл. 1 (1.8 – 1.17). 2. Г.Г. Поклад, С.П. Гриднев. Геодезия. Учебное пособие. – М.: Академический проект, 2007, §§ 8-20, 22-27. 3. Условные знаки для топографической карты масштаба 1: 10 000. М.: Недра, 1977. 4. Условные знаки для топографических планов масштабов 1: 5 000, 1: 2 000, 1: 1 000 и 1: 500. – М.: Недра, 1989. Начиная работу с картой, студент должен ознакомиться с зарамочным оформлением, номенклатурой, масштабом карты, оцифровкой градусной и километровой сеток, схемой, поясняющей взаимное расположение истинного, магнитного и осевого меридианов, и другими сведениями о карте. В процессе выполнения студентом расчетно-графической работы все результаты измерений, графических построений и расчетов должны быть аккуратно оформлены в рабочей тетради. При решении задач, связанных с графическими построениями, необходимые данные с карты (плана) копируют на кальку, на которой выполняют все последующие действия.
Задание 1. Определение горизонтальных расстояний с помощью масштабов Задача – познакомиться с видами основных масштабов и решить с их помощью практические задачи с оценкой точности линейных построений и определений. Принадлежности: карта масштаба 1: 10 000, циркуль-измеритель, масштабная линейка. Исходные данные: на учебной карте масштаба 1: 10 000 (рис. 1) заданы четыре точки (1, 2, 3, 4).
На картах и планах участки местности изображаются в уменьшенном виде. Степень уменьшения, выражаемая отношением длины отрезка на плане или карте (dпл.) к горизонтальной проекции соответствующей линии на местности (dмест), называется масштабом, т.е. Масштабы бывают численные и графические. Численный масштаб – аликвотная дробь, числитель которой единица, а знаменатель – число, показывающее, во сколько раз горизонтальные проекции линии местности уменьшены на плане или карте:
где М – знаменатель численного масштаба. В геодезической и землеустроительной практике наиболее часто применяются следующие масштабы: 1: 500, 1: 1 000, 1: 2 000, 1: 5 000 – для планов и 1: 10 000, 1: 25 000, 1: 50 000, 1: 100 000 и мельче – для топографических карт. На планах и картах под значением численного масштаба указывают именованный (пояснительный) масштаб в виде «в 1 сантиметре 20 метров» (для масштаба 1: 2 000). С помощью масштабов решают две основные задачи: 1. Определение горизонтальной проекции линии местности по длине отрезка на плане масштаба 1: М по формуле
2. Определение длины отрезка на плане масштаба 1: М, соответствующего горизонтальной проекции измеренной линии местности, по формуле
При решении этих задач используют специальные графические построения: линейный и поперечный (трансверсальный) масштабы. Обычно как линейный, так и поперечный масштабы имеют основание а = 2 см. Линейный масштаб – графическое изображение численного масштаба в виде прямой линии с делениями для отсчета расстояний (рис.2, а). Крайний левый отрезок делят на 10 равных частей и на правом его конце ставят 0, а на левом – число метров, которое на плане соответствует основанию в заданном масштабе. Вправо от 0-го деления подписывают значения соответствующих расстояний. В правом конце линейного масштаба ставят размерность. При работе с этим масштабом десятые доли малого деления оценивают на глаз. Расстояние на приведенном линейном масштабе равно 184, 8 м. Поперечный масштаб является разновидностью линейного масштаба и отличается от предыдущего более высокой точностью определения расстояния за счет применения трансверсалей («косых линий», рис. 2, б).
Рис. 2. Масштабы а) линейный; б) поперечный
На горизонтальной прямой несколько раз откладывают основание масштаба, равное 2 см. Из концов отложенных отрезков восставляют к прямой перпендикуляры равной длины (обычно по 2, 5 см). Крайние из них делят на 10 равных частей и соответствующие точки соединяют прямыми линиями. Затем крайнее левое основание и противолежащий ему верхний отрезок делят на 10 частей и точки деления соединяют наклонными линиями (трансверсалями). Такой поперечный масштаб называют нормальным сотенным масштабом, так как наименьшее деление масштаба (наименьший отрезок между перпендикуляром и трансверсалью) составляет 0, 01 основания масштаба, т.е. 0, 2 мм. Оцифровку делений поперечного масштаба выполняют по аналогии с линейным. При работе с поперечным масштабом нужно следить, чтобы иголки обеих ножек циркуля-измерителя располагались на одной горизонтальной линии масштаба либо посередине между одноименными горизонтальными линиями. Расстояние, показанное на поперечном масштабе (см. рис. 3, б), равно 184, 8 м. Оно складывается из трех частей: целого числа оснований (40м × 4 = 160 м), десятых долей основания масштаба (4м × 6 = 24 м) и сотых долей основания (вверх по трансверсали 0, 4м × 2 = 0, 8 м). При решении задач с использованием графических масштабов принимают, что практически длина отрезка на плане может быть оценена с точностью до 0, 2 мм. Горизонтальное расстояние на местности, соответствующее 0, 2 мм (0, 02 см) на плане данного масштаба, называется графической точностью масштаба, т.е.
Содержание задания 1. Выразить в форме именованного масштаба численные масштабы, наиболее часто применяемые на практике, и указать их графическую точность. Данные представить в виде таблицы (табл.1).
Таблица 1 Масштабы и их точность
2. Определить с помощью линейного масштаба, приведенного на листе карты (см. рис. 2) и металлического поперечного масштаба отрезки 1-2, 2-3, 3-4, 4-1, 1-3 и 2-4, заданные на топографической карте. Данные занести в табл. 2.
Таблица 2 Определение длин линий местности по карте
Примечание: вычисленные длины линий будут использованы в последующих заданиях.
|


 – масштаб.
– масштаб. , (1)
, (1)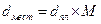
 .
.
 , м. (2)
, м. (2)


