И токов комплексными числами
При изображении вращающихся векторов синусоидальных величин на комплексно плоскости ось абсцисс плоскости декартовых координат совмещают с осью действительных или вещественных величин (ось + 1) комплексной плоскости. Тогда мгновенные значения синусоидальных величин получают на оси мнимых величин (ось+j). Каждому вектору на комплексной плоскости соответствует комплексное число, которое может быть записано в показательной, тригонометрической или алгебраической форме. Например, Э.Д.С.
Фазовый угол
Мнимая составляющая комплексного числа вектора на комплексной плоскости определяет синусоидальное изменение Э.Д.С. и обозначается символом
Комплексное число
Первое комплексное число
Второе комплексное число Следовательно,
Переход от одной формы записи синусоидальных величин к другой осуществляется с помощью формулы Эйлера Применение комплексных чисел позволяет от геометрического сложения или вычитания векторов на векторной диаграмме перейти к алгебраическому действию над комплексными числами этих векторов. Действующие и средние значения синусоидальных Э.Д.С.,
|
, соответствует комплексное число
.
определяют по проекциям вектора на оси координат +1 и +j:
.
:
.
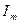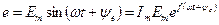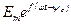удобно представить в виде произведения двух комплексных чисел:
.
, соответствующее положению вектора в начальный момент времени, называют комплексной амплитудой:
.
является оператором поворота вектора на угол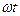 
относительного начального положения вектора.
.
.
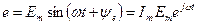