Метод эквивалентного преобразования соединений пассивных элементов звездой и треугольником
Встречаются схемы со сложным соединением элементов, которые нельзя отнести ни к параллельном, ни к последовательному соединению. Рассмотрим одну из таких схем, когда часть ее образует треугольник, вершинами которого являются три узла, а сторонами- три пассивных ветви, включенные между этими узлами. Для упрощения расчета подобных схем во многих случаях бывает удобно заменить треугольник эквивалентной трехлучевой звездой. Рассмотрим схему с двумя треугольниками резисторов Определим уравнения, связывающие сопротивления эквивалентных резисторов треугольника и звезды. Для этого воспользуемся общим условием эквивалентности, по которому токи в ветвях схемы, не подвергнутых преобразованию, должны оставаться без изменения. Это означает, что токи, направленные к узлам
Схема. Эквивалентные соединения резисторов треугольником (а) и звездой (б)
При обрыве провода, присоединенного к узлу а, напряжение между узлами В схеме треугольника между узлами
По условию эквивалентности
Повторяя вышеприведенные рассуждения для случая, когда обрывается провод, присоединенный к узлу
|

 и
и  . При замене этих треугольников эквивалентными звездами с сопротивлениями резисторов лучей
. При замене этих треугольников эквивалентными звездами с сопротивлениями резисторов лучей 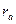 ,
,  ,
,  и
и  ,
,  ,
,  схема упрощается и приводится к схеме смешанного соединения.
схема упрощается и приводится к схеме смешанного соединения. ,
,  и
и  по проводам схем треугольника и звезды, должны быть одинаковыми. Условие эквивалентности должно быть соблюдено во всех режимах, в том числе при обрыве одного из проводов, присоединенных к узлам
по проводам схем треугольника и звезды, должны быть одинаковыми. Условие эквивалентности должно быть соблюдено во всех режимах, в том числе при обрыве одного из проводов, присоединенных к узлам  .
. , а в другую- два последовательно соединенных резистора с сопротивлениями
, а в другую- два последовательно соединенных резистора с сопротивлениями  и
и  . Общее сопротивление этой цепи
. Общее сопротивление этой цепи .
. .
.
 .
.


