Цепи с одним источником питания и параллельно соединенными пассивными приемниками
На рисунке показана схема с n пассивными ветвями, присоединенными к одним и тем же узлам А и В, разность потенциалов между которыми равна напряжению U источника. Поэтому ток в каждой n-ой ветви, определяется напряжением между узлами и сопротивлением rn или проводимостью
Схема цепи с параллельным соединением резистивных элементов (а) и ее эквивалентная схема (б)
……….…………………. (2.23)
То обстоятельство, что параллельное соединение обеспечивает одинаковое напряжение на всех включенных приемниках и их независимые друг от друга режимы работы, является важным преимуществом этого соединения, благодаря которому оно нашло широкое применение.
Подставляя в это уравнение значения токов из (2.23), получим выражение
Из которого можно вывести формулу эквивалентной проводимости
или формулу эквивалентного сопротивления
Представляет практический интерес цепь с двумя параллельно включенными резисторами, имеющими сопротивления
Токи ветвей этой цепи равны:
Согласно полученным соотношениям ток в одной из параллельных ветвей цепи равен току неразветвленного участка цепи, умноженному на отношение сопротивления противоположной ветви и суммы сопротивлений ветвей. Резистивный элемент с сопротивлением
Схема цепи со смешанным соединением резистивных элементов (а) и эквивалентные ей схемы (б) и (в)
Схема цепи, части которой образуют два треугольника резисторов (а), и эквивалентная ей схема (б)
Ток
Зная это напряжение, можно найти токи остальных ветвей:
Эти токи можно определить также по формулам
|
.
, 
.
,
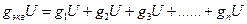(2.24)
и 
. Эквивалентное сопротивление такой цепи равно произведению сопротивлений, деленному на их сумму:
.
,
.
соединен последовательно с резистивным элементом с сопротивлением 
дает возможность определить общий ток 
исходной схемы.
проходит также по эквивалентному элементу с сопротивлением 
, падение напряжения на котором равно напряжению на участке DC исходной схемы:
.
и 
и 
.
