Электрическая цепь с реальной индуктивной катушкой
В реальной индуктивной катушке имеется ток
Необходимо установить закон изменения напряжения и на ее зажимах. Заменим реальную катушку пассивным двухполюсником, состоящим из последовательно соединенных r и L. Схема, треугольники напряжений и сопротивлений катушки с активным сопротивлением и индуктивностью
Согласно второму закону Кирхгофа имеем
Так как
Далее перейдем к уравнениям для комплексных значений напряжений и токов:
Тогда
Затем получим уравнение для комплексного напряжения на входе схемы:
или
В формулах, в которые величина
где,
где
Зная значения
Синусоида напряжения на входе катушки опережает по фазе синусоиду тока на угол сдвига Закон Ома для индуктивной катушки в комплексной форме:
Вектор напряжения на резисторе Векторную диаграмму называют треугольником напряжений. Из этого рисунка видно, что модуль z комплекса полного сопротивления Z является гипотенузой прямоугольного треугольника комплексных сопротивлений, сторонами которого является активное r и индуктивное
|

 .
. .
. и
и  являются синусоидальными имеют частоту
являются синусоидальными имеют частоту  . Напряжение
. Напряжение  может быть записано уравнением
может быть записано уравнением .
. .
. .
. и
и  .
. ,
, .
.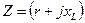 называют комплексом полного сопротивления индуктивной катушки.
называют комплексом полного сопротивления индуктивной катушки.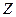 входит или как множитель или как делитель, удобно пользоваться не алгебраической, а показательной формой ее записи:
входит или как множитель или как делитель, удобно пользоваться не алгебраической, а показательной формой ее записи: ,
, - модуль комплекса полного сопротивления индуктивной катушки, а
- модуль комплекса полного сопротивления индуктивной катушки, а  - его аргумент.
- его аргумент. ,
, ,
,  .
. и
и  можно записать
можно записать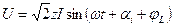 .
. .
. .
. совпадает по фазе с вектором тока, а вектор напряжения на индуктивном элементе
совпадает по фазе с вектором тока, а вектор напряжения на индуктивном элементе  опережает по фазе вектор тока на угол сдвига фаз
опережает по фазе вектор тока на угол сдвига фаз 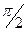 . Вектор напряжения
. Вектор напряжения  равен геометрической сумме векторов:
равен геометрической сумме векторов:  . Он опережает по фазе вектор тока на угол сдвига фаз
. Он опережает по фазе вектор тока на угол сдвига фаз  сопротивления. Из него же можно определить угол сдвига фаз:
сопротивления. Из него же можно определить угол сдвига фаз: .
.


