Решение одного уравнения
Для простейших уравнений вида f (x)=0 решение в Mathcad находится с помощью функции root. root(f (х 1, x 2, …), х 1, a, b) Возвращает значение х 1, принадлежащее отрезку [ a, b ], при котором выражение или функция f (х) обращается в 0. Оба аргумента этой функции должны быть скалярами. Функция возвращает скаляр. Аргументы: f (х 1, x 2, …) – функция, определенная где-либо в рабочем документе, или выражение. Выражение должно возвращать скалярные значения. х 1 – имя переменной, которая используется в выражении. Этой переменной перед использованием функции root необходимо присвоить числовое значение. Mathcad использует его как начальное приближение при поиске корня. a, b - необязательны, если используются, то должны быть вещественными числами, причем a < b. Если после многих итераций Mathcad не находит подходящего приближения, то появится сообщение Эта ошибка может быть вызвана следующими причинами: - уравнение не имеет корней, - корни уравнения расположены далеко от начального приближения, - выражение имеет локальные max и min между начальным приближением и корнями, - выражение имеет разрывы между начальными приближениями и корнями, - выражение имеет комплексный корень, но начальное приближение было вещественным. Чтобы установить причину ошибки, исследуйте график f (x). Он поможет выяснить наличие корней уравнения f (x) = 0 и, если они есть, то определить приблизительно их значения. Чем точнее выбрано начальное приближение корня, тем быстрее будет root сходиться. Рекомендации по использованию функции root: - Для изменения точности, с которой функция root ищет корень, нужно изменить значение системной переменной TOL. Если значение TOL увеличивается, функция root будет сходиться быстрее, но ответ будет менее точен. Если значение TOL уменьшается, то функция root будет сходиться медленнее, но ответ будет более точен. Чтобы изменить значение TOL в определенной точке рабочего документа, используйте определение вида - Если два корня расположены близко друг от друга, следует уменьшить TOL, чтобы различить их. - Если функция f (x) имеет малый наклон около искомого корня, функция root (f (x), x) может сходиться к значению r, отстоящему от корня достаточно далеко. В таких случаях для нахождения более точного значения корня необходимо уменьшить значение TOL. Другой вариант заключается в замене уравнения f (x) = 0на g (x) = 0
- Для выражения f (x) с известным корнем а нахождение дополнительных корней f (x) эквивалентно поиску корней уравнения h (x) = f (x)/(x - a). Подобный прием полезен для нахождения корней, расположенных близко друг к другу. Проще искать корень выражения h (x), чем пробовать искать другой корень уравнения f (x) = 0, выбирая различные начальные приближения. Задание 1. Решить уравнение cos(x)=x+0.2 с помощью функции root Решение:
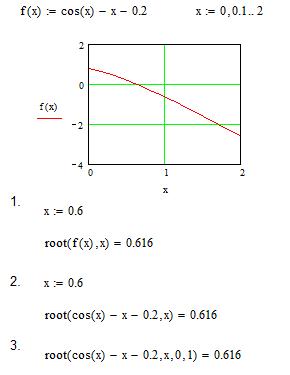
Рис. 1. Решение уравнения cos(x)= x-0.2
1 способ:
Функция вернет значение 0.6161 2 способ:
3 способ:
|

 (отсутствует сходимость).
(отсутствует сходимость).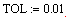 . Чтобы изменить значение TOL для всего рабочего документа, выберите команду Математика Параметры… Переменные Допуск сходимости (TOL).
. Чтобы изменить значение TOL для всего рабочего документа, выберите команду Математика Параметры… Переменные Допуск сходимости (TOL).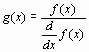 .
.