Безопасность жизнедеятельности. 1. Лабораторный практикум по технологическому оборудованию пищевых производств: Учеб
1. Лабораторный практикум по технологическому оборудованию пищевых производств: Учеб. пособие для вузов: С.Т. Антипов и др.; Воронеж, 1999. 2. Стабников В.Н. и др. Процессы и аппараты пищевых производств. М.: Агропромиздат, 1985. 3. Липатов Н.Н. Процессы и аппараты пищевых производств. М.: Экономика, 1987. 4. Проектирование процессов и аппаратов пищевых производств/ Под ред. В.Н. Стабников. – Киев: Вища школа, 1988.
С.В. Вендин Н.А.Жаворонко
IIроцессы и аппараты пищевых производств. Учебное пособие для лабораторно-практических занятий
Сданов печать 11.12.2007 г. Уч.-изд. л 0, 6 Ус.печ..л. 2, 5 Тираж экз. Заказ № ___ 308503 п.Майский Белгородская обл. Типография БелГСХА
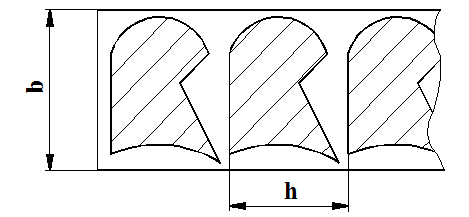
Оптимальный раскрой полос или штучных заготовок 2.1. Постановка задачи Однорядная штамповка деталей из ленты (полосы) определяется двумя параметрами: шириной половы b и шагом штамповки h (рис. 2.1.). Коэффициент использования металла h определяется для штамповки из полосы длиной l как отношение площади Sд n деталей, полученных из полосы, к площади полосы Sп (см. рис. 2.1.).
Рис. 2.1. Раскрой полосы на заготовки
При штамповке из ленты, когда длина ленты велика, концевые отходы можно не учитывать и коэффициент использования металла определяется как
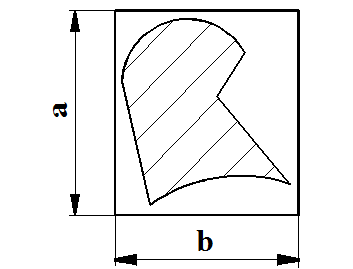
Рис. 2.2. Раскрой штучной заготовки
Под оптимальным раскроем в данном случае понимается нахождение таких величин h и b или a и b, при которых значение h максимально. 2.2. Математическое обеспечение 2.2.1. Кодирование контура заготовки
Для решения задачи оптимизации раскроя необходимо каким-либо образом описать контур исходной заготовки. В общем случае контур любой детали (заготовки) может быть представлен как произвольное сочетание прямоугольных и криволинейных элементов (рис. 2.3.) Криволинейные элементы могут быть представлены как совокупность дуг окружностей с различными радиусами. Для того чтобы описать заготовку, необходимо на её контуре найти узловые точки, то есть такие точки, в которых происходит смена линии, ограничивающей контур заготовки. Если координаты всех узловых точек, а также координаты центров кривизны дуг окружности известны, то описание контура можно задать перечислением в определённом порядке координат узловых точек и кодом характера линий между ними (см. рис. 2.3.)
2.2.2. Определение площади заготовки
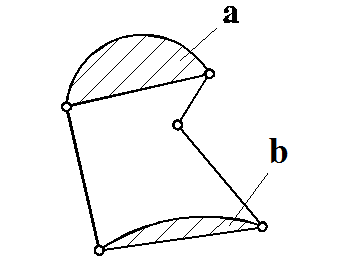
Для вычисления КИМ необходимо знать площадь заготовки. Так как фигура заготовки представлена в виде отрезков прямых и дуг окружности, то для определения площади фигуры её можно представить состоящей из площади многоугольника, к которой прибавляются (в случае выпуклой дуги) или отнимаются (в случае вогнутой дуги) площади сегментов (рис. 2.4.)
Рис. 2.3. Контур исходной заготовки
Рис. 2.4. Определение площади фигуры а – площадь прибавляется; b – площадь отнимается
Площадь многоугольника определяется по формуле
где
Для определения площади сегмента, находящегося между i-1 и i-той узловой точкой, вычислим величину радиуса дуги окружности:
где хцi, уцi – координаты центра дуги. Расстояние от i до i-1 точки найдём как
вычислим вспомогательную величину
Найдём величину центрального угла
Площадь сегмента вычисляется следующим образом:
где знак плюс ставится для выпуклой дуги, минус для вогнутой дуги. Площадь заготовки определяется как
где
2.2.3. Определение оптимального размера штучной заготовки
При вырубке детали из штучной заготовки контур детали должен целиком находиться внутри штучной заготовки (см. рис. 2.2.). Геометрически это означает, что вокруг контура заготовки описан прямоугольник. Если принять, что контур заготовки параллелен осям ОХ и ОУ, а деталь может занимать произвольное положение на плоскости, то каждому произвольному положению детали будет соответствовать заготовка с различными размерами. Пусть имеется деталь, заданная координатами узловых точек. Размер описанного прямоугольника будет зависеть от угла поворота ji детали относительно начального положения (рис. 2.5.)
Рис. 2.5. Исходная (I) и повёрнутая (II) деталь в штучной заготовке
Поворачивая контур детали на дискретный угол, получаем каждый раз новое значение: аi – ширины описанного прямоугольника; bi – длины описанного прямоугольника. Площадь описанного прямоугольника составляет
Коэффициент использования металла определяется по формуле
Из полученных значений Фигура задана массивом координат узловых точек, центров окружностей и кодами видов линий между узловыми точками. Так как работа с криволинейным контуром усложняет программу и удлиняет время расчёта, то предлагается прямые линии аппроксимировать отрезками прямых. Для этого создана специальная подпрограмма. Подпрограмма аппроксимации преобразует заданную информацию о контуре заготовки в массив координат узловых точек, между которыми находятся только отрезки прямых линий. Расчёт проводим в следующей последовательности. Фигура задана массивом координат узловых точек
При повороте фигуры на дискретный угол jI образуется новый массив точек
где хij и yij определяется как
Для определения размера заготовки необходимо найти точки с минимальными и максимальными значениями координат
По формуле (2.3) определяем коэффициент использования металла. Такой расчёт проводим для углов
2.2.4. Определение оптимального шага штамповки и ширины полосы
Метод решения задачи раскроя оптимальной штучной заготовки можно применить и для определения оптимального раскроя заготовки-полосы. Контур заготовки описывается последовательностью координат узловых точек, координат центров окружностей и кодов видов линий между узловыми точками. Как и для штучной заготовки, предлагается криволинейные элементы аппроксимировать отрезками прямых. В этом случае контур заготовки будет представлен совокупностью координат узловых точек. Необходимо определить оптимальную ширину полосы и шаг штамповки (рис. 2.6.). Направление оси полосы совпадает с направлением оси ОХ. Значение оптимального шага штамповки и ширины полосы зависит от угла поворота контура заготовки относительно направления штамповки. Рассмотрим размещение произвольного контура в полосе. Начальное положение контура задано совокупностью координат точек ( Сдвинутый контур описывается массивом точек
где
Рис. 2.6. Исходная (I) и повёрнутая (II) деталь в заготовке-полосе Из рис. 2.6. видно, что величина h лежит в пределах Для проверки условия непересечения контуров заготовок необходимо найти общие точки всех отрезков прямых, образующих контур сдвинутой фигуры. Уравнение прямой, проходящей через две точки с координатами (х1, у1), (х2, у2), имеет вид
После преобразования получаем
Введём обозначения:
С учётом принятых обозначений нахождение общих точек контуров сводится к решению системы линейных уравнений:
Если решение системы х и у и удовлетворяет следующим условиям:
то значит, что у фигур имеется, как минимум одна общая точка и условия укладки не выполняются. Необходимо увеличить расстояние h между фигурами. Величину h отыскиваем методом «двоичного поиска» в несколько шагов. Как было сказано, величина h лежит в пределах Этот процесс будем повторять до тех пор пока Величину b найдём как При повороте фигуры на угол
2.3.Ввод исходных данных
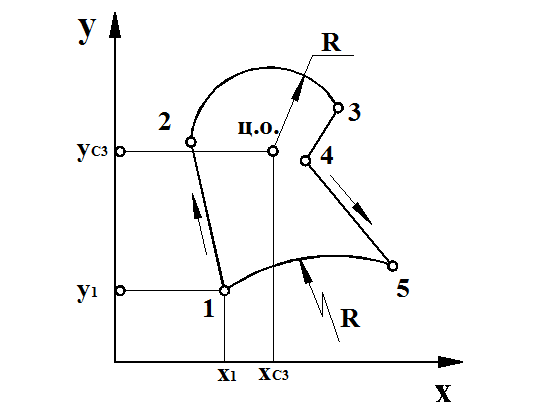
Ввод исходных данных осуществляется следующим образом. Контур заготовки представляется в виде отрезков прямых и дуг окружности и вычерчивается на листе миллиметровой бумаги в масштабе 1: 1. Далее проводятся линии ОХ и ОУ таким образом, чтобы контур заготовки оказался в первом квадрате (см. рис. 2.7.). Взяв какую-либо точку за начальную, необходимо пронумеровать точки в порядке обхода внутреннего контура против часовой стрелки (рис. 2.7.).
Рис. 2.7. Кодирование исходной заготовки
После этого необходимо присвоить линиям, соединяющим две соседние точки, определённый код. В зависимости от вида линии применяются следующие коды:
Далее определяются координаты точек и центров окружностей и заносятся в таблицу 2.1. В графу «Вариант» заносится:
Таблица 2.1.
Таблица заполняется следующим образом. Вначале заносятся номера и координаты точек, затем заносятся коды линии. Причём код определяется для линии, соединяющей текущую и предыдущую точки, например, для точки 2 код лдинии равен 0 (см. рис. 2.7.), для точки 3 код лини равен 2. Далее для тех точек, код которых равен 1 или 2, заносятся координаты центра окружности.
Безопасность жизнедеятельности
|

 .
.
 .
.
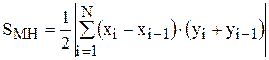 ,
,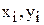 - координаты i-той точки;
- координаты i-той точки; - координаты i-той–1 точки
- координаты i-той–1 точки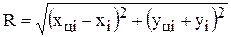 ,
, ,
, .
.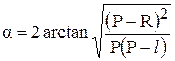 .
.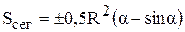 ,
,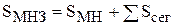 ,
, - сумма площадей сегментов.
- сумма площадей сегментов.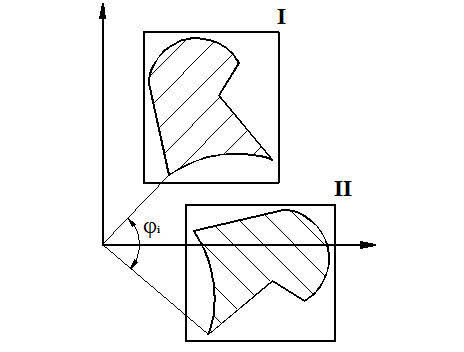
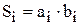 .
. .
. находим максимальное
находим максимальное 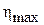 , соответствующие ему значения
, соответствующие ему значения 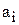 и
и  дадут размер оптимальной штучной заготовки.
дадут размер оптимальной штучной заготовки.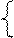 х1,
х1,
 хn
хn


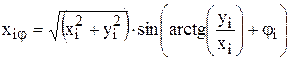
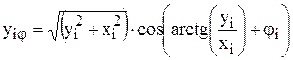
 ,
, 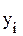 . По этим значениям находятся размеры заготовки:
. По этим значениям находятся размеры заготовки: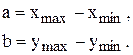
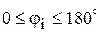 с определённым шагом (например, через 1°) и получаем множество значений
с определённым шагом (например, через 1°) и получаем множество значений  для каждого угла поворота
для каждого угла поворота 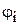 . Из полученного множества значений
. Из полученного множества значений 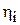 находим максимальное
находим максимальное  . Соответствующие этому значению КИМ величины
. Соответствующие этому значению КИМ величины 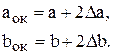
 и
и 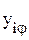 . Для определения шага штамповки необходимо узнать, на какую минимальную величину hmin необходимо сдвинуть контур относительно исходного положения, чтобы соседние заготовки не накладывались друг на друга. Это означает, что заготовки не должны иметь общих точек.
. Для определения шага штамповки необходимо узнать, на какую минимальную величину hmin необходимо сдвинуть контур относительно исходного положения, чтобы соседние заготовки не накладывались друг на друга. Это означает, что заготовки не должны иметь общих точек.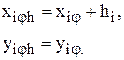

 , где
, где  определяется как
определяется как 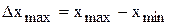 .
.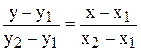 .
.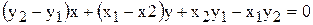 .
.
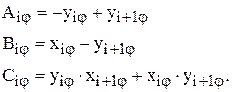


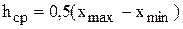 . Шаг 2. Если для этого
. Шаг 2. Если для этого 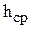 фигуры пересекаются, то сделаем
фигуры пересекаются, то сделаем  и перейдём к шагу 1. Если фигуры не пересекаются, то сделаем
и перейдём к шагу 1. Если фигуры не пересекаются, то сделаем  и перейдём к шагу 1.
и перейдём к шагу 1.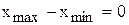 ; тогда величинаh будет равна hопт.
; тогда величинаh будет равна hопт.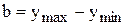 . По формуле (2.2.) вычислим коэффициент использования металла.
. По формуле (2.2.) вычислим коэффициент использования металла.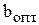 будут оптимальными.
будут оптимальными.



