Примеры гидравлических расчетов
Пример 1.1. В отопительной системе (котел, радиаторы, трубопроводы) частного дома содержится V = 0, 3 м3 воды. Сколько воды дополнительно войдет в расширительный бак при нагревании от 20 до 80°С. Решение: Плотность воды при температуре t 1 = 20°С до t 2 = 80°С определим по таблице 4.1 (приложение 4):
Масса воды при начальной температуре
Объем, занимаемый водой при t 2 = 80°С
Таким образом, дополнительный объем составляет
Пример 1.2. В отопительный котел поступает 50 м3воды при температуре t 1 = 70°С. Какой объем V воды будет выходить из котла при нагреве воды до t 2 = 90°С. Решение: Из формулы получаем дополнительный объем воды при нагревании
Коэффициент температурного расширения находим по таблице 4.4 (Приложение 4): Следовательно, Таким образом, из котла при нагревании будет выходить объем воды
Пример 1.3. Определить среднюю толщину δ известковых отложений в герметичном водоводе внутренним диаметром d = 0, 3 м и длиной l = 2 км. При выпуске воды в количестве Δ V =0, 05 м3 давление в водоводе падает на величину Δ p = 106 Па. Считать, что отложения по диаметру и длине водовода распределены равномерно. Решение: Из формулыβ p =
Коэффициент объемного сжатия воды находим по табл.4.2 (Приложение 4) Тогда С другой стороны объем водовода с отложениями
Откуда выразим внутренний диаметр водовода с отложениями
Средняя толщина отложений
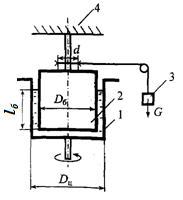
Задачи Задача 1.1. Определить плотность жидкости ρ, полученной смешиванием объема жидкости V 1= 0, 02 м3 плотностью ρ 1 = 910 кг/м3 и объема жидкости V 2= 0, 03 м3 плотностью ρ 2 = 850 кг/м3. Задача 1.2. Определить плотность топливной смеси (по весу) при следующем составе: керосин (ρ к = 775 кг/м3) – 40%, мазут (ρ м = 870 кг/м3) – 60%. Задача 1.3. При гидравлическом испытании трубопровода длиной L = 1000 м и диаметром d = 100 мм давление поднималось от p 1 = 1 МПа до p 2 = 1, 5 МПа. Определить объем жидкости Δ V, который был дополнительно закачан в водопровод. Коэффициент объемного сжатия β P = 4, 75·10-10 1/Па. Задача 1.4. При гидравлическом испытании трубопровода диаметром d = 0, 4 м длиной L = 20 м и давление воды сначала было p 1 = 5, 5 МПа. Через час давление упало до p 2 = 5, 0 МПа. Определить, пренебрегая деформацией трубопровода, сколько воды вытекло при этом через неплотности. Коэффициент объемного сжатия β P = 4, 75·10-10 1/Па. Задача 1.5. Как изменится объем воды в системе отопления, имеющей вместимость V = 100 м3, после подогрева воды от начальной температуры t 1 = 15 °C до t 2 = 95 °C. Коэффициент температурного расширения β t = 0, 00072 1/°С. Задача 1.6. Трубопровод диаметром d = 500 мм и длиной L = 1000 м наполнен водой при давлении p 1 = 400 кПа, и температуре воды t 1 = 5 °C. Определить, пренебрегая деформациями и расширением стенок труб, давление в трубопроводе при нагревании воды в нем до t 2 = 15 °C, если коэффициент объемного сжатия β P = 5, 18·10-10 1/Па, а коэффициент температурного расширения β t = 150·10-6 1/°С. Задача 1.7. Определить повышение давления, при котором начальный объем воды уменьшится на 3%. Коэффициент объемного сжатия воды β P = 4, 75·10-10 1/Па. Задача 1.8. При гидравлических испытаниях (проверке герметичности) подземного трубопровода длиной L = 500 м, диаметром d = 0, 1 м давление в нем повысилось от от p 1 = 0 до p 2 = 1, 0 МПа. Пренебрегая деформацией стенок трубопровода, определить объем воды, которую необходимо дополнительно закачать в трубопровод. Объемный модуль упругости воды принять равным Е = 2000 МПа. Задача В.9. В трубопровод вместимостью 50 м3 во время испытаний было дополнительно закачано 0, 05 м3 воды. Определить приращение давления в трубопроводе, если объемный модуль упругости воды Е = 2·109 Па. Задача В.10. Винтовой плунжерный насос для тарировки манометров работает на масле с коэффициентом объемного сжатия β р = 0, 625·10-9 1/Па. Определить на сколько оборотов надо повернуть маховик винта, чтобы поднять Задача 1.11. Резервуар заполнен жидкостью, объем которой V = 8 м3. Определить коэффициент температурного расширения жидкости β t, если при увеличении температуры от t 1 = 10 °С до t 2 = 20 °С объем жидкости увеличился на 6 л. Задача 1.12. В отопительный котел поступает объем воды V = 80 м3 при температуре t 1 = 60 °С. Какой объем воды V 1 будет выходить из котла при нагреве воды до температуры t 2 = 90 °С. Задача 1.13. Для периодического аккумулирования дополнительного объема воды, получающегося при изменении температуры, к системе водяного отопления в верхней ее точке присоединяют расширительные резервуары, сообщающиеся с атмосферой. Определить наименьший объем расширительного резервуара, чтобы он полностью не опоражнивался. Допустимое колебание температуры воды во время перерывов в топке Δ t = 30 °C. Объем воды в системе V = 0, 7 м3. Коэффициент температурного расширения воды при средней температуре t = 80 °С β t = 6·10-4 1/°С. Задача 1.14. Определить среднюю толщину отложений в герметичном водоводе внутренним диаметром d = 0, 5 м и длиной l = 3 км. При выпуске воды объемом Δ V = 0, 08 м3 давление в водоводе падает на Δ р = 1 МПа. Отложения по диаметру и длине водовода распределены равномерно. Коэффициент объемного сжатия воды сжатия β р = 5·10-10 1/Па. Задача 1.15. Стальной водовод диаметром d = 0, 4 м и длиной l = 1 км, проложенный открыто, находится под давлением р = 2 МПа при температуре воды t 1 = 10 °С. Определить давление воды в водоводе при повышении температуры до t 2 = 15 °С в результате наружного прогрева. Задача 1.16. Определить изменение плотности воды при увеличении давления от p 1 = 100 кПа до p 2 = 10000 кПа. При изменении давления температура воды не изменяется, коэффициент объемного сжатия β р = 5·10-10 1/Па. Задача 1.17. В отопительной системе дома содержится V = 0, 4 м3 воды при температуре t 1 = 15°C. Определить объем воды, который дополнительно войдет в расширительный бачок при повышении температуры до t 2 = 90°С. Задача 1.18. Определить изменение плотности воды при изменении температуры от t 1 = 5 °С до t 2 = 95 °С. Задача 1.19. Вязкость нефти, определенная вискозиметром, составила 4 °Е, а ее плотность ρ =880 кг/м3. Определить кинематический и динамический коэффициенты вязкости нефти. Задача 1.20. Определить ротационным вискозиметром вязкость жидкости плотностью ρ = 920 кг/м3. Вес груза G = 80 Н, диаметры цилиндра D ц = 225 мм, барабана D б = 223 мм, шкива d = 200 мм. Глубина погружения барабана в жидкость lб = 250 мм. Время опускания груза t гр = 12 с, путь l гр = 300 мм.
Примечание: Схема ротационного вискозиметра: в цилиндре 1 установлен барабан 2, вращающийся под действием опускающегося груза 3. Цилиндр закреплен на основании 4. Контрольные вопросы и задания
1. Охарактеризуйте строение жидкости, ее сходство и различие с твердым телом. 2. Перечислите свойства жидкости, важные для практики. 3. Какую жидкость называют идеальной? В каких случаях в практических расчетах жидкость можно считать идеальной? 4. Чем объясняется малая сжимаемость жидкостей? Почему они не сохраняют свою форму? 5. В каких случаях необходимо учитывать свойство температурного расширения жидкостей? 6.Что называется вязкостью? Какими параметрами характеризуется вязкость жидкости? 7. Как зависит вязкость жидкости от температуры и давления?
|



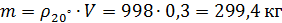
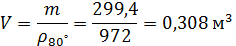
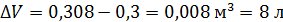 .
.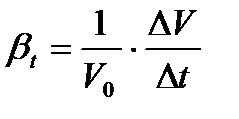
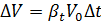
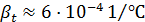 .
.
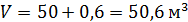
 , определим объем воды в водоводе с отложениями:
, определим объем воды в водоводе с отложениями:
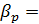 5·10-10 1/Па
5·10-10 1/Па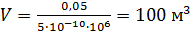
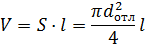


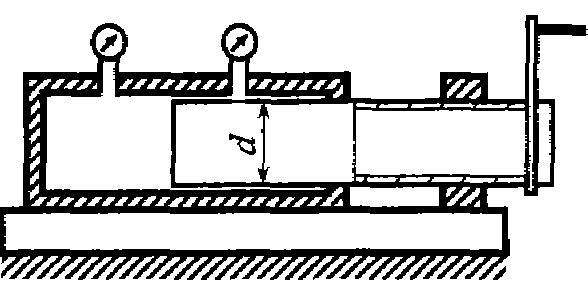 давление внутри насоса на Δ p = 0, 1 МПа, если объем рабочей камеры пресса V = 628 см3, диаметр плунжера d = 20 мм, шаг винта h = 2 мм. Стенки рабочей камеры считать недеформируемыми.
давление внутри насоса на Δ p = 0, 1 МПа, если объем рабочей камеры пресса V = 628 см3, диаметр плунжера d = 20 мм, шаг винта h = 2 мм. Стенки рабочей камеры считать недеформируемыми.