Правила построения и контроля правильности построения эпюр внутренних силовых факторов
Из рассмотренных примеров, как следствия дифференциальных зависимостей между 1. В сечениях, где приложены сосредоточенные силы, на эпюрах продольной и поперечной сил происходит скачек на величину этих сил в направлении их действия, а эпюра изгибающего момента претерпевает излом в сторону действия сосредоточенных сил. 2. На участках стержней, где отсутствует равномерно распределенная нагрузка, продольная и поперечная сила величины постоянные, а эпюра изгибающего момента изменяется по закону наклонной прямой. 3. На участках, где приложена равномерно распределенная нагрузка, эпюры продольной и поперечной сил изменяются по закону наклонной прямой на величину равнодействующей распределенной нагрузки. При положительном значении распределенной нагрузки эпюры возрастают, при отрицательном – убывают. 4. В сечениях на свободном или шарнирно опертом концах балки, где отсутствует сосредоточенный изгибающий момент, изгибающий момент равен нулю. 5. На участках, где приложена поперечная равномерно распределенная нагрузка, эпюра изгибающего момента изменяется по закону квадратной параболы, выпуклостью навстречу направлению действия распределенной нагрузки. 6. В сечениях, где приложен сосредоточенный изгибающий момент, на эпюре изгибающего момента происходит скачек на его величину в направлении его действия. 7. В сечении, где поперечная сила равна нулю, изгибающий момент имеет экстремальное значение. 8. На участках, где поперечная сила равна нулю, изгибающий момент величина постоянная. 9. На участках, где поперечная сила положительна, эпюра изгибающего момента возрастает, где отрицательна – убывает. 10. Изгибающий момент в любом сечении равен площади эпюры поперечной силы левой или правой отсеченной части балки плюс приложенные к ним сосредоточенные изгибающие моменты.
Вопросы и ответы для самоконтроля 1. Что называется главным вектором внутренних сил? Равнодействующий вектор внутренних сил, приложенный в центре тяжести сечения, называется главным вектором внутренних сил. 2. Что называется главным моментом внутренних сил? Равнодействующий момент внутренних сил, действующий относительно центра тяжести сечения, называется главным моментом внутренних сил. 3. Что называется внутренними силовыми факторами? Проекции главного вектора и главного момента внутренних сил на оси подвижной системы координат, помещенной началом в центре тяжести сечения, называются внутренними силовыми факторами. 4. Гипотеза плоских сечений. Сечения плоские и перпендикулярные оси стержня до деформации при простых состояниях стержня, остаются плоскими и перпендикулярными оси стержня после деформации. 5. Чему равна продольная сила в любом сечении?
6. Чему равны поперечные силы в любом сечении?
7. Чему равен крутящий момент в любом сечении?
8. Чему равны изгибающие моменты в любом сечении?
9. Что показывают эпюры внутренних силовых факторов? Эпюры внутренних силовых факторов показывают графический закон их изменения вдоль продольной оси стержня. 10. Для чего строятся эпюры внутренних силовых факторов? Эпюры внутренних силовых факторов строятся для определения закона их изменения по длине стержня и определения сечений с их максимальным значением. 11. Какое состояние называется растяжением-сжатием? Состояние стержня, при котором в его сечениях действует продольная сила, называется растяжением-сжатием. 12. Какое состояние называется чистым сдвигом? Состояние стержня, при котором в его сечениях действует поперечная сила, называется чистым сдвигом. 13. Какое состояние называется кручением? Состояние стержня, при котором в его сечениях действует крутящий момент, называется кручением. 14. Какое состояние называется чистым изгибом? Состояние стержня, при котором в его сечениях действует только изгибающий момент, называется чистым изгибом. 15. Какое состояние называется поперечным изгибом? Состояние стержня, при котором в его сечениях действует одновременно поперечная сила и изгибающий момент, называется поперечным изгибом. 16. Системы подвижных координат для отсеченных частей стержня. Рисунок 3.12
Рисунок 3.12 17. Правила знаков при определении внутренних силовых факторов. Рисунок 3.12 Проекции внешних продольных сил положительны, если они направлены от рассматриваемого сечения. Проекции внешних поперечных сил положительны, если они направлены вверх слева от сечения и вниз справа от сечения. Крутящий момент от внешних нагрузок положителен, если он действует по часовой стрелке относительно оси z любой отсеченной части стержня. Изгибающий момент от внешних нагрузок положителен, если он действует по часовой стрелке относительно поперечной оси слева от сечения и против часовой стрелке справа от сечения. 18.Дифференциальные зависимости между интенсивностью внешних распределенных нагрузок и внутренними силовыми факторами.
19. Дифференциальные зависимости между внутренними силовыми факторами.
|

 ,
,  и
и  , вытекают следующие правила.
, вытекают следующие правила.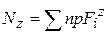 - продольная сила в любом сечении равна алгебраической сумме проекций всех внешних сил, действующих на отсеченную часть стержня, на продольную ось z.
- продольная сила в любом сечении равна алгебраической сумме проекций всех внешних сил, действующих на отсеченную часть стержня, на продольную ось z.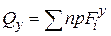 ,
, 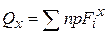 - поперечные силы в любом сечении равны алгебраической сумме проекций всех внешних сил, действующих на отсеченную часть стержня, на поперечные оси y, x.
- поперечные силы в любом сечении равны алгебраической сумме проекций всех внешних сил, действующих на отсеченную часть стержня, на поперечные оси y, x.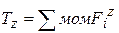 - крутящий момент в любом сечении равен алгебраической сумме моментов всех внешних сил, действующих на отсеченную часть стержня, относительно оси z.
- крутящий момент в любом сечении равен алгебраической сумме моментов всех внешних сил, действующих на отсеченную часть стержня, относительно оси z. ,
, 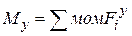 - изгибающие моменты в любом сечении равны алгебраической сумме моментов всех внешних сил, действующих на отсеченную часть стержня, относительно осей х, y.
- изгибающие моменты в любом сечении равны алгебраической сумме моментов всех внешних сил, действующих на отсеченную часть стержня, относительно осей х, y.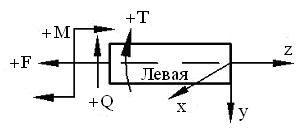

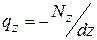 ,
, 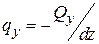 ,
,  ,
,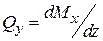 ,
, 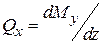 .
.


