Ход решения
1. Определяем реакцию опоры.
2. Разбиваем стержень на участки с постоянным законом изменения внешних нагрузок. Стержень имеет три участка АВ, ВС и СD. 3. Составляем уравнения продольной силы по участкам. Для участка АВ Для участка ВС
Рисунок 3.6
Для участка DC 4. По найденным значениям строим эпюру продольной силы в соответствии с рисунком 3.6 б. Примечание. Чтобы не определять реакцию опоры необходимо по всем 3 участкам рассматривать левые отсечённые части стержня.
Пример 5 Построить эпюру крутящего момента для вала, нагруженного внешними моментами По данным варианта задания вычертить в масштабе расчётную схему вала с указанием величин моментов и размеров участков. Ход решения. 1. Определяем реакцию опоры. На вал действует система внешних крутящих моментов относительно продольной оси z. Поэтому в жёстко защемлённой опоре возникает только реактивный крутящий момент
2. Разбиваем стержень вала на участки с постоянным законом изменения внешних нагрузок. Для данного вала имеем три участка АВ, ВС и СD, на которых изменения моментных нагрузок не происходит. 3. Составляем уравнения крутящего момента по участкам. Приложенные к валу крутящие моменты вызывают в его сечениях действие только крутящего момента. Крутящий момент в любом сечении вала равен алгебраической сумме крутящих моментов всех внешних сил, действующих на отсечённую часть вала, относительно продольной оси z. При этом крутящий
Рисунок 3.7 момент от внешних нагрузок считается положительным для правой и левой отсечённых частей, если он действует по часовой стрелке относительно оси z отсеченной части вала, в соответствии с рисунком 3.7 в. Для участка АВ проводим в любом месте участка сечение и видим, что выгодно рассматривать левую отсечённую часть.
Для участка ВС Для участка DC выгодно рассматривать правую отсечённую часть 4. По найденным значениям строим эпюру крутящего момента по всей длине вала в соответствии с рисунком 3.7 б.
Пример 6 Построить эпюры поперечной силы и изгибающего момента для шарнирно опертой балки, загруженной внешними нагрузками По данным варианта задания вычертить в масштабе расчётную схему балки с указанием величин нагрузок и размеров участков.
Ход решения. 1. Определяем реакции опор. В шарнирно неподвижной опоре под действием внешних нагрузок возникает вертикальная реакция RA и горизонтальная реакция НА, в шарнирно подвижной опоре – только вертикальная реакция RC. Так как на балку действуют только вертикальные внешние нагрузки, то горизонтальная реакция НА =0. Вертикальные реакции RA, RC определяются из сумм моментов всех внешних сил относительно опор А, С.
Знаки плюс значений реакций показывают, что их направление выбрано верно. При получении знака минус для значения какой-либо реакции её
Рисунок 3.8 направление изменить на обратное. Проводим проверку правильности определения значений реакций опор. Для этого составим уравнение суммы проекций всех внешних сил на вертикальную ось у
Следовательно, реакции определены верно. 2. Разбиваем балку на участки с постоянным законом изменения внешних нагрузок. Для данной балки получаем три участка. Участки АВ и ВС, на которых действует равномерно распределённая нагрузка, и участок CD без изменения внешней нагрузки. 3. Составляем уравнения поперечной силы и изгибающего момента по участкам. Приложенные к балке внешние вертикальные (поперечные) нагрузки вызывают в её сечениях действие поперечной силы Изгибающий момент относительно оси х в любом сечении равен алгебраической сумме моментов всех внешних сил, действующих на отсечённую часть балки, относительно оси х. Изгибающий момент от внешней нагрузки принимается положительным, если он действует относительно оси х по часовой стрелке для левой отсечённой части и против часовой стрелки для правой отсечённой части. Для участка АВ выгодно рассматривать левую отсечённую часть
Определяем первую производную от уравнения изгибающего момента Определяем вторую производную Для участка ВС
Так как на участке ВС имеется сечение, где
Для участка DС выгодно рассматривать правую отсечённую часть
4. По найденным значениям строим эпюры поперечной силы 3.8 б. Для этого проводим ось эпюры параллельно оси балки и положительные значения поперечной силы и изгибающего момента откладываем вверх, отрицательные – вниз. Примечание: Для строительных специальностей по правилам строительной механики ординаты эпюры изгибающих моментов откладывают со стороны растянутых слоев. Поэтому положительные значения изгибающего момента откладываются вниз и эпюра Мх на участках АВ и ВС изменяется выпуклостью вниз.
Пример № 7 Построить эпюры поперечной силы и изгибающего момента для консольной балки, нагруженной внешними нагрузками = 5 кН, М = 20 кНм. Длина участков а = 1 м, b = 3 м, с = 2 м, в соответствии с рисунком 3.9 а. Ход решения 1. Определяем реакции опор.
Проверка 2. Разбиваем балку на три участка АВ, ВС и СD. 3. Составляем уравнения внутренних силовых факторов по участкам. Для участка АВ
Для участка ВС
Рисунок 3.9
Для участка DС
4. По найденным значениям строим эпюры поперечной силы и изгибающего момента по всем участкам балки в соответствии с рисунком 3.9 б. Примечание - В этой задаче можно не определять реакции опор RD и Мр. В этом случае построение эпюр внутренних силовых факторов для участка DС нужно проводить из рассмотрения левой отсечённой части.
Пример № 8 Построить эпюры внутренних силовых факторов для рамы, нагруженной внешними нагрузками По данным варианта задания вычерчиваем в масштабе расчетную схему рамы с указанием величин нагрузок и размеров участков.
Ход решения. 1. Определяем реакции опор:
Проверка 2. Разбиваем раму на два участка АВ и ВС. 3. Составляем уравнения внутренних силовых факторов по участкам. Приложенные к раме внешние нагрузки вызывают в ее сечениях действие продольной Nz, поперечной Оси подвижной системы координат для левых отсеченных частей рамы: ось z вправо от сечения, ось y в сечении вертикально вниз, ось x в сечении горизонтально к наблюдателю, для правых отсеченных частей оси направлены противоположно. Положение системы координат на любом последующем участке рамы получается путем поворота системы координат предыдущего участка в плоскости сопряженных стержней. Для участка АВ
Исследуем эпюру
Рисунок 3.10
Для участка СВ
По найденным значениям строим эпюры
5 Проводим проверку правильности построения эпюр внутренних силовых факторов в узлах рамы. Для этого вырезаем узел В и прикладываем к нему внешние нагрузки и внутренние силовые факторы, действующие в сечениях вырезанного узла, в соответствии с рисунком 3.10 в. Составляем уравнения равновесия узла.
Пример № 9 Построить эпюры внутренних силовых факторов для рамы, нагруженной внешними нагрузками Ход решения. 1. Определяем реакции опор:
Проверка 2. Рама имеет 4 участка с постоянным законом изменения внешних нагрузок АВ, ВС, СD и СЕ. 3. Составляем уравнения продольной и поперечной сил и изгибающего момента по участкам. Для участка АВ
Для участка ВС
Исследуем уравнение Тогда
Для участка DС
Для участка ЕС
3. По найденным значениям строим эпюры
Рисунок 3.11
5. Проводим проверку для узлов в соответствии с рисунком 3.11 в.
|

 Отсюда
Отсюда .
.
 - уравнение прямой.
- уравнение прямой. 
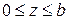

 - уравнение прямой
- уравнение прямой 


 .
. . Длина участков а = 0, 3 м, b = 0, 4 м, с = 0, 3 м, в соответствии с рисунком 3.7 а.
. Длина участков а = 0, 3 м, b = 0, 4 м, с = 0, 3 м, в соответствии с рисунком 3.7 а. . Для определения его величины составляем уравнение моментов относительно оси z для всего вала
. Для определения его величины составляем уравнение моментов относительно оси z для всего вала 
 Отсюда
Отсюда  .
.
 ,
,  - величина по длине участка постоянная.
- величина по длине участка постоянная. .
.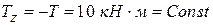 .
.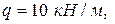


 . Длина участков а = 1 м, b = 3 м, с = 2 м, в соответствии с рисунком 3.8 а.
. Длина участков а = 1 м, b = 3 м, с = 2 м, в соответствии с рисунком 3.8 а. Отсюда
Отсюда
 Отсюда
Отсюда

 .
.
 и изгибающего момента
и изгибающего момента  . Поперечная сила в любом сечении равна алгебраической сумме проекций всех внешних сил, действующих на отсечённую часть балки, на ось у. Проекция внешней нагрузки или её равнодействующей на вертикальную ось у принимается положительной, если она слева от сечения направлена вверх, справа – вниз, в соответствии с рисунком 3.8 в.
. Поперечная сила в любом сечении равна алгебраической сумме проекций всех внешних сил, действующих на отсечённую часть балки, на ось у. Проекция внешней нагрузки или её равнодействующей на вертикальную ось у принимается положительной, если она слева от сечения направлена вверх, справа – вниз, в соответствии с рисунком 3.8 в. - уравнение прямой
- уравнение прямой 
 - уравнение квадратной параболы.
- уравнение квадратной параболы. 
 .
. . Следовательно, эпюра Мх на участке АВ изменяется по закону квадратной параболы выпуклостью вверх.
. Следовательно, эпюра Мх на участке АВ изменяется по закону квадратной параболы выпуклостью вверх. - уравнение прямой
- уравнение прямой 
 - уравнение квадратной параболы.
- уравнение квадратной параболы.
 , то в этом сечении на эпюре Мх изгибающий момент имеет экстремальное значение. Подсчитаем его величину
, то в этом сечении на эпюре Мх изгибающий момент имеет экстремальное значение. Подсчитаем его величину Отсюда
Отсюда 

 < 0, выпуклость эпюры Мх вверх
< 0, выпуклость эпюры Мх вверх .
. - уравнение прямой
- уравнение прямой 
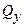 и изгибающего момента
и изгибающего момента  по всем участкам балки в соответствии с рисунком
по всем участкам балки в соответствии с рисунком F =
F = = 0 Отсюда
= 0 Отсюда
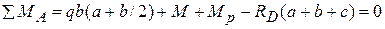 Отсюда
Отсюда .
. . Реакции определены верно.
. Реакции определены верно.
 - уравнение прямой
- уравнение прямой 
 - уравнение прямой
- уравнение прямой 

 - уравнение квадратной параболы
- уравнение квадратной параболы 
 Отсюда
Отсюда  .
. .
.  , выпуклость эпюры Мх вверх.
, выпуклость эпюры Мх вверх. - величина постоянная.
- величина постоянная.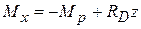 - уравнение прямой
- уравнение прямой 
 кН/м,
кН/м,  кН,
кН,  кНм. Длина участков
кНм. Длина участков  м,
м,  м, в соответствии с рисунком 3.10 а.
м, в соответствии с рисунком 3.10 а. Отсюда
Отсюда  кН
кН Отсюда
Отсюда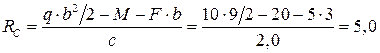 кН
кН Отсюда
Отсюда кН
кН . Реакции определены верно.
. Реакции определены верно. сил и изгибающего момента Mx. Эпюры для каждого участка рам строят по правилам и уравнениям, принятым для прямых стержней. При составлении уравнений силовых факторов наблюдатель располагается в плоскости чертежа внутри контура рамы и обращен к рассматриваемому сечению, для которого составляются уравнения.
сил и изгибающего момента Mx. Эпюры для каждого участка рам строят по правилам и уравнениям, принятым для прямых стержней. При составлении уравнений силовых факторов наблюдатель располагается в плоскости чертежа внутри контура рамы и обращен к рассматриваемому сечению, для которого составляются уравнения. кН -
кН - 
 -уравнение прямой
-уравнение прямой 

 - уравнение квадратной параболы
- уравнение квадратной параболы  .
. Отсюда
Отсюда  м. Тогда
м. Тогда кН
кН  м,
м, выпуклость эпюры
выпуклость эпюры  вверх.
вверх.
 ,
, 
 - уравнение прямой
- уравнение прямой 
 и
и 


 кН/м,
кН/м,  кН,
кН,  кН
кН 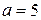 м, b =3, 0 м, c =2, 0 м, в соответствии с рисунком 3.11 а.
м, b =3, 0 м, c =2, 0 м, в соответствии с рисунком 3.11 а. Отсюда
Отсюда  кН
кН Отсюда
Отсюда кН
кН Отсюда
Отсюда кН
кН
 кН -
кН -  кН -
кН -  - уравнение прямой
- уравнение прямой 
 кН -
кН -  - уравнение прямой
- уравнение прямой 
 - уравнение квадратной параболы
- уравнение квадратной параболы 
 Отсюда
Отсюда  м.
м. кН
кН  - выпуклость эпюры
- выпуклость эпюры  ,
,  кН -
кН - 
 кН -
кН - 
 и
и