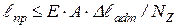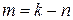Простые состояния стержней
Состояние растяжения - сжатия. Основные понятия Состояние стержня, при котором в его сечениях действует только продольная сила, называется растяжением-сжатием. Рисунок 4.1. Если продольная сила положительна стержень испытывает состояние растяжения, если
Рисунок 4.1 отрицательна – сжатия. При растяжении-сжатии все продольные слои поперечных сечений стержня получают одинаковую абсолютную деформацию Величина абсолютной деформации определяется по формуле
где Для одного участка стержня с постоянными величинами продольной силы и площади поперечного сечения абсолютная деформация
Условие прочности при растяжении-сжатии записывается формулой где
Для определения характеристик прочности и пластичности материалов проводят их испытания на растяжение. В результате получают диаграммы условных напряжений. Их вид для углеродистой стали Ст.3 и хрупких материалов показаны на рисунках 4.2 а, б. Напряжения, действующие в сечениях образца, характеризуют способность материала сопротивляться упругим и упруго-пластическим деформациям вплоть до разрыва, и являются характеристиками прочности материала. На участке диаграммы 0-1 происходят только упругие деформации, прямо пропорциональные действующим напряжениям, т.е. справедлив закон Гука площадкам наклонным под углом 450 к оси образца. Явление увеличения пластической деформации при постоянном напряжении называется текучестью. Напряжение Максимальное условное напряжение
Рисунок 4.2 Пластические свойства материала определяются величинами:
где
Если в точке К диаграммы произвести разгрузку образца, то разгрузка будет происходить по линии КВ почти параллельно участку пропорциональности. При повторном нагружении образца его загружение происходит по прямой ВК, на которой происходят только упругие деформации и далее по кривой К, 3, 4, где происходят упругие и пластические деформации. Явление увеличения участка пропорциональности BK и предела пропорциональности
По условию прочности Проектировочная задача определения размеров поперечного сечения Проверочная задача определения допустимой величины продольной силы Проверочная задача определения максимальных напряжений и коэффи-циента запаса прочности Условие жесткости для стержня с одним участком записывается формулой Проектировочная задача определения размеров сечения Проверочная задача определения величины допускаемой продольной силы Проверочная задача проверки жесткости Проектировочная задача определения предельной длины участка стержня При расчетах встречаются статически неопределимые системы. Системы, в которых число неизвестных реакций опор больше числа уравнений равновесия статика, называются статически неопределимыми. Разность между числом неизвестных реакций опор и числом уравнений равновесия статики называется степенью статической неопределимости системы.
где k – число неизвестных реакций опор; n – число уравнений равновесия статики. Реакции, лишние по отношению к числу уравнений равновесия статики, называются «лишними» реакциями. Для раскрытия статической неопределимости составляются дополнительно к числу уравнений равновесия статики системы уравнения совместности перемещений (деформаций) по числу «лишних» реакций. Для этого составляются основная и эквивалентная системы. Рисунок 4.5. Основной называется статически определимая, геометрически неизменяемая система, полученная из статически неопределимой, путем отбрасывания «лишних» реакций опор вместе с внутренними или внешними связями опор. Эквивалентной называется основная система, к которой приложены «лишние» реакции без связей. И определение реакций статически неопределимой системы проводится из совместного решения уравнений равновесия статики и дополнительных уравнений совместности перемещений.
|


 . Мерой ее величины является относительная продольная деформация
. Мерой ее величины является относительная продольная деформация  , которая по площади поперечного сечения распределяется равномерно. На основании закона Гука
, которая по площади поперечного сечения распределяется равномерно. На основании закона Гука  в поперечных сечениях будет действовать нормальные напряжения
в поперечных сечениях будет действовать нормальные напряжения  , которые по сечению распределяются равномерно. Коэффициент Е – модуль нормальной упругости является характеристикой упругих свойств материала, величина постоянная для каждого материала, характеризует способность материала сопротивляться упругим деформациям при растяжении-сжатии. В поперечном направлении происходит уменьшение размеров поперечного сечения на величину абсолютной поперечной деформации
, которые по сечению распределяются равномерно. Коэффициент Е – модуль нормальной упругости является характеристикой упругих свойств материала, величина постоянная для каждого материала, характеризует способность материала сопротивляться упругим деформациям при растяжении-сжатии. В поперечном направлении происходит уменьшение размеров поперечного сечения на величину абсолютной поперечной деформации  . Мерой ее величины является относительная поперечная деформация
. Мерой ее величины является относительная поперечная деформация 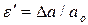 . Для изотропных материалов отношение относительной упругой поперечной и продольной деформаций является величиной постоянной, которая определяется коэффициентом поперечной деформации
. Для изотропных материалов отношение относительной упругой поперечной и продольной деформаций является величиной постоянной, которая определяется коэффициентом поперечной деформации 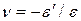 . Из этой формулы получается закон Пуассона
. Из этой формулы получается закон Пуассона 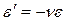 - относительная поперечная упругая деформация прямо пропорциональна относительной продольной упругой деформации. Знак минус показывает, что эти деформации противоположны.
- относительная поперечная упругая деформация прямо пропорциональна относительной продольной упругой деформации. Знак минус показывает, что эти деформации противоположны.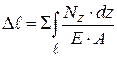 ,
, - жесткость стержня при растяжении-сжатии, характеризует способность стержня сопротивляться упругим деформациям при растяжении-сжатии.
- жесткость стержня при растяжении-сжатии, характеризует способность стержня сопротивляться упругим деформациям при растяжении-сжатии. Для нескольких участков
Для нескольких участков 
 .
.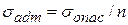 - допускаемое напряжение для материала элемента конструкции;
- допускаемое напряжение для материала элемента конструкции; - опасное напряжение, равное пределу текучести
- опасное напряжение, равное пределу текучести  для пластичных материалов и пределу прочности
для пластичных материалов и пределу прочности  для хрупких материалов;
для хрупких материалов; - коэффициент запаса прочности.
- коэффициент запаса прочности.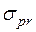 , до которого справедлив закон Гука, называется пределом пропорциональности. На горизонтальном участке диаграммы при постоянном напряжении
, до которого справедлив закон Гука, называется пределом пропорциональности. На горизонтальном участке диаграммы при постоянном напряжении 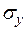 происходят только пластические деформации, за счет деформаций сдвига, происходящих по
происходят только пластические деформации, за счет деформаций сдвига, происходящих по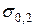 , равный напряжению при котором остаточная относительная деформация образца
, равный напряжению при котором остаточная относительная деформация образца  , т.е. 0, 2 %.
, т.е. 0, 2 %.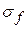 , при котором происходит разрыв образца, называется напряжением разрушения.
, при котором происходит разрыв образца, называется напряжением разрушения.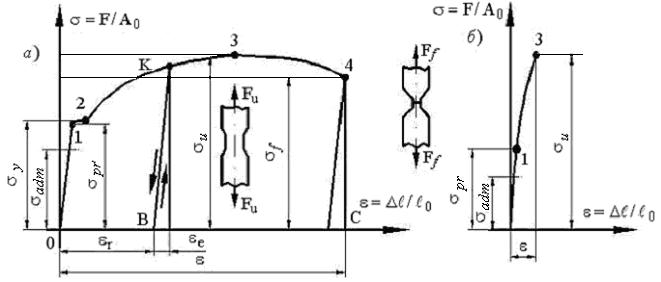
 - относительное остаточное удлинение, пластичность материала в продольном направлении;
- относительное остаточное удлинение, пластичность материала в продольном направлении; - относительное остаточное сужение площади поперечного сечения, пластичность материала в поперечном направлении.
- относительное остаточное сужение площади поперечного сечения, пластичность материала в поперечном направлении. - длина расчетной части образца;
- длина расчетной части образца; - абсолютная остаточная деформация расчетной длины образца;
- абсолютная остаточная деформация расчетной длины образца; - первоначальная площадь поперечного сечения расчетной части образца;
- первоначальная площадь поперечного сечения расчетной части образца;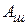 - площадь поперечного сечения шейки образца.
- площадь поперечного сечения шейки образца. в результате предварительной пластической деформации материала называется наклепом.
в результате предварительной пластической деформации материала называется наклепом. решаются три задачи сопротивления материалов.
решаются три задачи сопротивления материалов. .
.
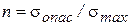
 . По условию жесткости решаются четыре задачи сопротивления материалов.
. По условию жесткости решаются четыре задачи сопротивления материалов.