Ход решения. 1. Определяем реакцию опоры
1. Определяем реакцию опоры. Так как на жестко защемленный стержень действуют только продольные внешние нагрузки, то в жёсткой защемленной опоре А возникает только горизонтальная реакция НА. Составляем сумму проекций всех внешних сил на продольную ось стержня
Знак плюс в ответе показывает, что направление реакции НА проставлено на расчётной схеме верно. Если в ответе получится знак минус, то направление реакции нужно изменить на обратное. 2. Разбиваем стержень на участки с постоянным законом изменения внешних нагрузок. Стержень имеет три участка. Участки АВ и СD, на которых нет изменения внешних нагрузок, и участок ВС, на котором закон изменения равномерно распределённой нагрузки q постоянен. 3. Составляем уравнения продольной силы по всем участкам. Так как на стержень действуют только продольные внешние нагрузки, то в любом сечении стержня они вызывают действие только продольной силы Nz. На участке АВ в произвольном месте проводим поперечное сечение. Для составления уравнения Nz выгодно рассматривать левую отсечённую часть, так как на неё действует меньше внешних нагрузок - только реакция Для участка АВ Для участка СВ в произвольном месте проводим сечение. Для составления уравнения Nz выгодно рассматривать всю правую отсечённую часть стержня с системой координат x, y, z для правой отсечённой части. На всю правую отсечённую часть действует внешняя сосредоточенная сила F и равнодействующая равномерно распределённой нагрузки
При При Для участка DС выгодно рассматривать правую отсечённую часть длиной 4. По найденным значениям строим эпюру продольной силы по всей длине стержня в соответствии с рисунком 3.5б. Для этого проводим ось эпюры параллельно оси стержня и откладываем положительные значения Примечания: 1. При выполнении расчётно-проектировочных работ пояснения к решению задач и чертежи отсечённых частей приводить не обязательно. 2. Реакцию опоры можно не определять, если на всех участках рассматривать правые отсеченные части.
Пример 4 Построить эпюру продольной силы для стержня нагруженного внешними нагрузками q = 10 кН/м, F = 5, 0 кН. Длина участков а = 0, 8 м, b = 1, 2 м, с = 0, 4 м, в соответствии с рисунком 3.6.
|


 Отсюда
Отсюда  кН
кН . Обозначаем длину отсечённой части z и показываем её отдельно. Помещаем в центре тяжести рассматриваемого сечения подвижную систему координат x, y, z для левой осечённой части и составляем уравнение продольной силы. Продольная сила в любом сечении равна алгебраической сумме проекций всех внешних сил, действующих на отсечённую часть стержня, на продольную ось z. При составлении уравнений пользуемся правилом знаков: проекция внешней нагрузки положительна, если она направлена от рассматриваемого сечения (растягивает отсечённую часть от рассматриваемого сечения) и отрицательна, если она направлена к сечению (сжимает отсечённую часть к сечению), в соответствии с рисунком 3.5 в.
. Обозначаем длину отсечённой части z и показываем её отдельно. Помещаем в центре тяжести рассматриваемого сечения подвижную систему координат x, y, z для левой осечённой части и составляем уравнение продольной силы. Продольная сила в любом сечении равна алгебраической сумме проекций всех внешних сил, действующих на отсечённую часть стержня, на продольную ось z. При составлении уравнений пользуемся правилом знаков: проекция внешней нагрузки положительна, если она направлена от рассматриваемого сечения (растягивает отсечённую часть от рассматриваемого сечения) и отрицательна, если она направлена к сечению (сжимает отсечённую часть к сечению), в соответствии с рисунком 3.5 в.
 , т.е. величина по всей длине участка постоянная.
, т.е. величина по всей длине участка постоянная. .
. . Продольная сила на этом участке изменяется по закону прямой.
. Продольная сила на этом участке изменяется по закону прямой. в сечении С
в сечении С  .
. в сечении В
в сечении В 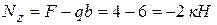 .
. .
.  .
. вверх, отрицательные – вниз.
вверх, отрицательные – вниз.


