Расчетно-проектировочная работа № 1
«Геометрические характеристики плоских сечений»
Пример 1. Определить главные центральные моменты инерции и построить эллипс инерции составного сечения, показанного на рисунке 2.4 Разбиваем составное сечение на составляющие типовые сечения и определяем геометрические характеристики относительно их собственных центральных осей в соответствии с рисунком 2.5. Для швеллера № 10 по ГОСТ 8240-89 Для пластины Для неравнобокого уголка № 7, 5/5, 0´ 0, 5 по ГОСТ 8510-86 с учетом изменения положения осей
Рисунок 2.4
Рисунок 2.5
Центробежный момент инерции сечения неравнобокого уголка относительно собственных центральных осей определяется по формуле
- где знак минус центробежного момента инерции определяется по его знакам в квадрантах относительно собственных центральных осей
Ход решения
Вычерчиваем в масштабе составное сечение по заданному варианту задания и проводим вспомогательную систему координат x, y. Рисунок 2.4. 1. Определяем положение центра тяжести составного сечения относительно вспомогательной системы координат х, у.
где
По найденным координатам строим положение центра тяжести составного сечения и проводим вспомогательные центральные оси х 0, у 0 параллельно вспомогательным осям х, у. 2. Определяем моменты инерции составного сечения относительно вспомогательных центральных осей х 0, у 0. Осевые моменты инерции
Центробежный момент инерции
где - расстояния между собственными центральными осями типовых сечений и вспомогательными центральными осями 3. Определяем положение главных центральных осей
Строим положение главных центральных осей u, v откладывая угол a относительно осей 4. Определяем значение главных моментов инерции составного сечения
Проводим проверку правильности определения главных моментов инерции. Центробежный момент инерции относительно главных центральных осей
По закону постоянства суммы осевых моментов инерции
5. Определяем радиусы инерции эллипса инерции относительно главных осей u, v.
По найденным радиусам инерции строим эллипс инерции, откладывая их значения относительно соответствующих осей. Пример 2. Определить главные центральные моменты инерции и построить эллипс инерции составного сечения, показанного на рисунке 2.6 Разбиваем составное сечение на составляющие типовые сечения и определяем геометрические характеристики относительно их собственных центральных осей. Рисунок 2.7. Для горизонтальных пластин b1= 20 см, h1= 1, 0 см, А1= b1
Для вертикальных пластин Для неравнобоких уголков № 7, 5/5, 0´ 0, 5 по ГОСТ 8510-86
Рисунок 2.6
Рисунок 2.7
Центробежный момент инерции сечения неравнобокого уголка относительно собственных центральных осей определяется по формуле:
Ход решения
Вычерчиваем в масштабе составное сечение по заданному варианту задания. Рисунок 2.6.
1. Определяем положение центра тяжести составного сечения. Так как сечение симметрично относительно осей х0, у0, то эти оси являются главными центральными осями сечения и Площадь составного сечения см 2 2. Определяем моменты инерции составного сечения относительно главных центральных осей х 0, у 0.
- где
Так как составное сечение симметрично относительно обеих центральных осей, то центробежный момент инерции сечения относительно этих осей равен нулю. 3. Определяем радиусы инерции эллипса инерции составного сечения относительно главных центральных осей
По найденным радиусам инерции строим эллипс инерции, откладывая их значения относительно соответствующих осей.
Вопросы и ответы для самоконтроля 1. Чему равен статический момент площади сечения относительно оси.
2. Чему равен статический момент составного сечения относительно какой-либо оси?
3. Формулы для определения положения центра тяжести сечения.
4. Перечислить формулы для определения осевых моментов инерции типовых сечений относительно собственных центральных осей (прямоугольник, прямоугольный треугольник, круг, кольцо). 5. Формулы перехода к параллельным осям для осевых моментов инерции сечения.
6. Какие оси сечения называются главными центральными осями? Оси сечения, относительно которых осевые моменты инерции имеют экстремальные значения ( 7. Закон постоянства суммы осевых моментов инерции сечения.
8. Формулы для определения главных моментов инерции сечения.
9. Формулы для определения положения главных центральных осей
|

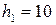 см,
см,  см,
см,  см 2,
см 2,  см 4,
см 4, 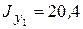 см 4,
см 4,  см,
см,  .
. =20, 0 см,
=20, 0 см,  см,
см,  см 2,
см 2, 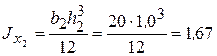 см 4;
см 4;  см 4;
см 4; 
 ;
; 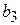 =7, 5 см;
=7, 5 см;  = 5, 0 см;
= 5, 0 см;  =6, 11 см 2;
=6, 11 см 2; = 12, 5 см 4;
= 12, 5 см 4;  =34, 8 см 4;
=34, 8 см 4;  =2, 39 см;
=2, 39 см;  =1, 17 см;
=1, 17 см;  =0, 436;
=0, 436;  =23036¢
=23036¢


 см;
см;  см
см
 см 3 – статический момент площади составного сечения относительно вспомогательной оси у;
см 3 – статический момент площади составного сечения относительно вспомогательной оси у;
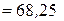 см 3 – статический момент площади составного сечения относительно вспомогательной оси х;
см 3 – статический момент площади составного сечения относительно вспомогательной оси х; см 2 – площадь составного сечения;
см 2 – площадь составного сечения; =1, 44 см;
=1, 44 см;  =10, 0 см;
=10, 0 см;  =17, 61 см;
=17, 61 см;  =6, 0 см;
=6, 0 см;  =0, 5 см;
=0, 5 см;  = -1, 17 см – координаты центров тяжести типовых сечений относительно вспомогательных осей х, у.
= -1, 17 см – координаты центров тяжести типовых сечений относительно вспомогательных осей х, у.
 см 4
см 4
 см 4
см 4


 см,
см,  см,
см,  см,
см, 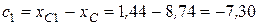 см,
см,  см,
см, 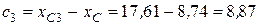 см,
см,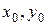 составного сечения.
составного сечения. ;
; 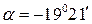
 . Ось u откладывается от оси
. Ось u откладывается от оси 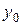 и ось v от оси
и ось v от оси  , т.к.
, т.к.  а
а  . Знак минус показывает, что угол
. Знак минус показывает, что угол  откладывается по часовой стрелке.
откладывается по часовой стрелке.

 см4 ;
см4 ; 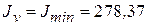 см 4
см 4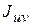 =0.
=0.

 2283, 27 см 4 = 2283, 28 см 4
2283, 27 см 4 = 2283, 28 см 4 см,
см, 
 h1= 20
h1= 20  ,
, 
 =1, 0 см,
=1, 0 см,  см,
см,  см 2
см 2  см 4;
см 4;  см 4;
см 4; 
 =5 см;
=5 см; = 7, 5 см;
= 7, 5 см;  =6, 11 см 2;
=6, 11 см 2;  =1, 17 см;
=1, 17 см;  =2, 39 см;
=2, 39 см;  =0, 436;
=0, 436;  =23036¢
=23036¢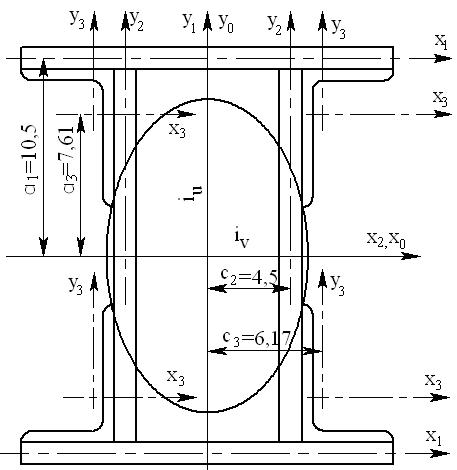


 .
.

 см 4 =
см 4 = 

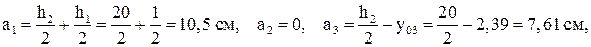
 - расстояния между собственными центральными осями типовых сечений и главными центральными осями
- расстояния между собственными центральными осями типовых сечений и главными центральными осями  составного сечения.
составного сечения. см,
см,  см,
см,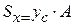 ,
,  . Статический момент площади сечения относительно какой-либо оси равен произведению площади сечения на координату ее центра тяжести до этой оси
. Статический момент площади сечения относительно какой-либо оси равен произведению площади сечения на координату ее центра тяжести до этой оси ,
,  Статический момент составного сечения относительно какой-либо оси равен алгебраической сумме статических моментов типовых сечений составного сечения относительно этой же оси.
Статический момент составного сечения относительно какой-либо оси равен алгебраической сумме статических моментов типовых сечений составного сечения относительно этой же оси. ,
,  Координата центра тяжести сечения относительно какой-либо оси равна статическому моменту площади сечения относительно этой оси деленному на площадь сечения.
Координата центра тяжести сечения относительно какой-либо оси равна статическому моменту площади сечения относительно этой оси деленному на площадь сечения. ,
,  Осевой момент инерции сечения относительно оси, параллельной центральной оси сечения, равен сумме осевого момента инерции сечения относительно собственной центральной оси и произведения площади сечения на квадрат расстояния между осями
Осевой момент инерции сечения относительно оси, параллельной центральной оси сечения, равен сумме осевого момента инерции сечения относительно собственной центральной оси и произведения площади сечения на квадрат расстояния между осями ), а центробежный момент инерции равен нулю, называются главными центральными осями.
), а центробежный момент инерции равен нулю, называются главными центральными осями. . Сумма осевых моментов инерции относительно любых взаимно перпендикулярных центральных осей сечения равна сумме главных моментов инерции и есть величина постоянная, равная полярному моменту инерции сечения
. Сумма осевых моментов инерции относительно любых взаимно перпендикулярных центральных осей сечения равна сумме главных моментов инерции и есть величина постоянная, равная полярному моменту инерции сечения  .
.
 или
или  .
.


