Решение задачи традиционными методами. Построение математической модели

 

Построение математической модели. Суммарные затраты, связанные с распределением объемов финансирования Х_ij из каждого i-ro источника в каждом j-ом периоде, можно записать в таком виде: m n

. (3.3.1.2)

Совокупность систем линейных ограничений (см.выше), граничных условий (3.3.1.1) и линейной целевой функции (3.3.1.2) образует математическую модель задачи, которую часто называют транспортной.

Рассмотрим один из эффективных алгоритмов решения транспортной задачи метод потенциалов. В качестве начального допустимого решения опорного плана возьмем план, приведенный в табл. 3.3.1.2.

Основой вычислительного процесса (алгоритма) этого метода является определение критерия оптимальности вида:

где C_ij – фактические затраты, связанные с выделением единицы денежных ресурсов из i-ro источника в j-ом периоде,

Z_ij - расчетные затраты, связанные с выделением единицы денежных ресурсов из i-ro источника в j-ом периоде.

Расчетные затраты Z_ij определяются только для клеток, куда финансовые ресурсы не распределены.

Если все d_ij > 0 (i = l_, 2,..., m), (j = 1, 2,..., n), то полученное допустимое решение (опорный план) является оптимальным_, если нет_, то с помощью этого критерия оптимизации можно указать способ улучшения решения.

 

Таблица 3.3.1.2

	B1	B2	B3	B4	a
A1	0 70	0 38	0 24	0 92
A2	0 58	20 18	0 56	0 72
A3	23 19	2 10	1 100	0 30
A4	7 3	0 36	0 121	34 8
bj

 

Алгоритм решения.

Алгоритм решения включает следующие основные этапы:

1. Составление и решение системы уравнений. Вводятся условные цены-оценки единицы ресурса для каждого поставщика U_i (i = 1, 2,..., m) и каждого потребителя V (j = 1, 2,..., n). Эти оценки или, как их чаще называют_, потенциалы выступают в задаче как локальные цены (или наценки к единой цене), создающие заинтересованность в правильном распределении ресурсов. Так_, цена в пункте потребления Vj равна цене в пункте поставщика U_j плюс наценка С_ij. В нашей задаче наценка С_ij представляет собой дополнительные затраты на выделение единицы ресурса из i-ro источника в j-ом периоде. Таким образом:

^V_J = ^U₁ + C_1J.

С целью нахождения значений V_j (j = 1, 2,..., n) и U_i (i = 1, 2,..._, m) составляются уравнения для клеток, в которые распределены ресурсы в опорном плане:

V₃ – U₁ = C₁₃ = 24

V₂ – U₂ = C₂₂ = 18

V₁ – U₃ = C₃₁ = 19

V₂ – U₃ = C₃₂ = 10

V₁ – U₄ = C₄₁ = 3

V₃ - U₃ = C₃₃ = 100;

V₄ - U₄ = C₄₄ = 8.

Мы имеем 7 уравнений и 8 неизвестных, поэтому одной из искомых переменных наиболее часто встречающейся в уравнениях, для облегчения счета необходимо присвоить произвольное значение равное нулю. В нашей системе уравнений чаще всех встречается переменная U₃. Предположим, U₃ = 0. Последовательно решая соответствующие уравнения, получим: V, = 19, V₂ = 10, V₃ = 100, U, = 76, U₂ = - 8, U₄ = 16, V₄ = 24.

2. Определение расчетных значений Z_ij.

Z_ij = V_j - U_i

При этом используются те индексы i и j, на пересечении которых в соответствующих клетках ресурсы не распределены;

Z₁₁ = V₁ – U₁ = 19 - 76 = -57;

Z₁₂ = V₂ – U₁ = 10 - 76 = -66;

Z₁₄ = V₄ – U₁ = 24 – 76 = -52;

Z₂₁ = V₁ - U₂ = 19 + 8 = 27;

Z₂₃ = V₃ - U₂ =100 + 8 = 108;

Z₂₄ = V₄ - U₂ = 24 + 8 = 32;

Z₃₄ = V₄ - U₃ = 24 + 0 = 24;

Z₄₂ = V₂ - U₄ = 10 - 16 = -6;

Z₄₃ = V₃ - U₄ = 100 - 16 = 84.

 

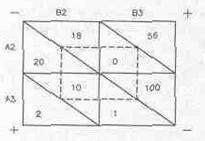
3. Определение значений d_t и проверка условия оптимальности.

Если все d > 0 (i = 1, 2,..., m), (j = 1, 2,..., п), то полученное допустимое решение (опорный план) является оптимальным, если нет, то переходят к новому:

d₁₁ = C₁₁ – Z₁₁ = 70 + 57 = 127;

d₁₂ = C₁₂ - Z₁₂ = 38 + 66 = 104;

d₁₄ – С₁₄ – Z₁₄ = 92 + 52 = 144;

d₂₁ = C₂₁ - Z₂₁ = 58 - 27 = 31;

d₂₃ = C₂₃ - Z₂₃ = 56-108 = -52;

d₂₄ = C₂₄ - Z₂₄ = 72 - 32 = 40;

d₃₄ = C₃₄ - Z₃₄ = 30 - 24 = 6;

d₄₂ = C₄₂ - Z₄₂ = 36 + 6 = 42;

d₄₃ = C₄₃ - Z₄₃ = 121 - 84 = 37.

В нашей задаче не все d₂₃ > 0, а это означает, что решение еще неоптимально, и мы переходим к определению нового опорного плана.

4. Определение нового опорного плана с меньшим значением целевой функции. Для этого в решение вводится та переменная X_ij, которой отвечает наименьшее отрицательное значение d_ij. Вводя ее, одновременно изменяют величины других переменных, по меньшей мере в трех заполненных клетках, чтобы не нарушались итоговые величины в строках и столбцах таблицы - a., b. Для этого строят многоугольник, одна из вершин которого находится в свободной клетке, а остальные - в заполненных ресурсами (загруженных). Для этой вершины d_ij < 0 и имеет наименьшее значение. При этом все углы многоугольника должны быть прямыми. Перемещение ресурсов производят в пределах клеток, лежащих в вершинах многоугольника (рис. 3.3.1.1). Если для свободной клетки поставить знак + (плюс), а в следующей вершине - (минус), затем снова + и т.д., поочередно изменяя знак, то в нее переносится меньшее из чисел, стоящих в клетках с отрицательными знаками. В результате она, как основная переменная, исключается из опорного плана. Одновременно необходимо установить равновесие по всему многоугольнику.

Если использовать правило перераспределения ресурсов в пределах многоугольника, распределение будет выглядеть, как на рис. 3.3.1.2.

Рис. 3.3.1.1 Схема перераспределения ресурсов.

Рис. 3.3.1.2. Схема перераспределенных ресурсов.

При этом сумма ресурсов по всем строкам и столбцам осталась без изменений. Проводя соответствующие преобразования в исходном допустимом решении (плане), получим новый опорный план (табл. 3.3.1.3).

В результате построения нового допустимого решения (начального плана) способом потенциалов величина критерия оптимизации (целевой функции) будет равна:

Y = 14 х 24 + 19 х 18 + 1 х 56 + 23 X 19 + 3 X 10 + 7 х 3 + 34 х 8 = 1494.

Нахождением нового опорного плана заканчивается первое приближение (итерация). Далее все этапы повторяются.

 

Таблица 3.3.1.3

 

	B1	B2	B3	B4	a
A1	0 70	0 38	14 24	0 92
A2	0 58	19 18	1 56	0 72
A3	23 19	3 10	0 100	0 30
A4	7 3	0 36	0 121	34 8
bj