ПРИЛОЖЕНИЕ ТЕОРИИ ВЕРОЯТНОСТИ К ОБРАБОТКЕ РЕЗУЛЬТАТОВ ИЗМЕРЕНИЙ
Пусть для определения неизвестной физической постоянной а производится n независимых измерений, причем считается, что грубые и систематические ошибки отсутствуют (см. § 6, п. 2). Возможный результат каждого из n измерений есть случайная величина, которую мы обозначим через  (i — номер измерения). Так как каждое измерение не зависит от результатов других измерений, то мы имеем n случайных независимых величин (i — номер измерения). Так как каждое измерение не зависит от результатов других измерений, то мы имеем n случайных независимых величин  . Обозначим через x1, x2,..., xn фактически полученные результаты n измерений величины а. Таким образом, xi есть одно из возможных значений . Обозначим через x1, x2,..., xn фактически полученные результаты n измерений величины а. Таким образом, xi есть одно из возможных значений  . .
На основании закона больших чисел Чебышева (см, § 5, п. 2) мы можем утверждать, что с практической достоверностью для достаточно большого числа n измерений средняя арифметическая результатов измерений отличается от истинного значения физической постоянной сколь угодно мало, т. е. с вероятностью, сколь угодно близкой к единице, имеет место приближенное равенство

Оценим точность этого приближенного равенства. Для этого прежде всего заметим, что в силу основного закона ошибок (см. § 6, п. 2) каждый возможный результат измерения  есть случайная величина, подчиняющаяся нормальному закону распределения вероятностей с одним и тем же математическим ожиданием, равным истинному значению а измеряемой величины: есть случайная величина, подчиняющаяся нормальному закону распределения вероятностей с одним и тем же математическим ожиданием, равным истинному значению а измеряемой величины:  (i=1, 2,..., n). Далее будем предполагать, что все измерения проводятся с одинаковой степенью точности (равноточные измерения). Поэтому дисперсии всех случайных величин должны быть одинаковыми, т. е. (i=1, 2,..., n). Далее будем предполагать, что все измерения проводятся с одинаковой степенью точности (равноточные измерения). Поэтому дисперсии всех случайных величин должны быть одинаковыми, т. е.  . .
Сначала рассмотрим случай оценки неизвестного значения а, предполагая известным значение  . Так как возможный результат i -гo измерения есть случайная величина . Так как возможный результат i -гo измерения есть случайная величина  , подчиняющаяся нормальному закону распределения вероятностей с математическим ожиданием , подчиняющаяся нормальному закону распределения вероятностей с математическим ожиданием  и дисперсией и дисперсией  , то случайная величина , то случайная величина  также имеет нормальное распределение с тем же математическим ожиданием также имеет нормальное распределение с тем же математическим ожиданием  , и средним квадратическим отклонением , и средним квадратическим отклонением  (см. § 4, п. 3). Поэтому плотность распределения вероятностей для средней арифметической (см. § 4, п. 3). Поэтому плотность распределения вероятностей для средней арифметической  имеет вид имеет вид

где параметры распределения равны а и 
Следовательно, вероятность того, что при n измерениях мы получим такую совокупность значений  , что при любом , что при любом  интервал интервал  будет содержать а, на основании формулы (33) определяется соотношением будет содержать а, на основании формулы (33) определяется соотношением

| (58)
| Интервал  имеет случайные границы имеет случайные границы  и и  . Соотношение (58) справедливо для любого значения . Соотношение (58) справедливо для любого значения  . Вероятность . Вероятность  не зависит от конкретных значений, которые принимают случайные величины не зависит от конкретных значений, которые принимают случайные величины  и при возрастании числа измерений n в силу свойства функции Ф(х) возрастает (см. § 3, п. 4). Соотношение (58) показывает, что каковы бы ни были значения x1, x2,..., xn полученные при измерении, имеет место формула и при возрастании числа измерений n в силу свойства функции Ф(х) возрастает (см. § 3, п. 4). Соотношение (58) показывает, что каковы бы ни были значения x1, x2,..., xn полученные при измерении, имеет место формула

| (59)
| где  . Величина . Величина  называется средней выборочной. Формулой (59) в большинстве случаев пользоваться нельзя, так как обычно значение называется средней выборочной. Формулой (59) в большинстве случаев пользоваться нельзя, так как обычно значение  неизвестно. Поэтому рассмотрим случай, когда обе величины а и неизвестно. Поэтому рассмотрим случай, когда обе величины а и  неизвестны. неизвестны.
Пусть случайная величина s2 определена соотношением

| (60)
| где  . Можно показать, что величина s2 имеет математическое ожидание, равное . Можно показать, что величина s2 имеет математическое ожидание, равное  , и дисперсию, равную , и дисперсию, равную  , т.е. , т.е.

(доказательство не приводим ввиду громоздкости вычислений). Применим к случайной величине s2 вторую лемму Чебышева (см. § 5, п. 1):

где  . Подставляя значения M(s2) и D(s2), получим . Подставляя значения M(s2) и D(s2), получим
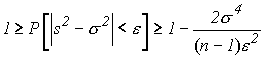
| (61)
|
Соотношение (61) показывает, что если  , то , то  , т.е. s2 стремится по вероятности к , т.е. s2 стремится по вероятности к  . .
Рассмотрим величину

Так как  есть одно из возможных значений s2, то при достаточно больших n с практической достоверностью можно утверждать, что имеет место приближенное равенство есть одно из возможных значений s2, то при достаточно больших n с практической достоверностью можно утверждать, что имеет место приближенное равенство

| (62)
| где  . Величину . Величину  называют выборочной дисперсией. называют выборочной дисперсией.
На практике для оценки вероятности того, что истинное значение а измеряемой величины лежит в интервале  , пользуются формулой (59), где вместо , пользуются формулой (59), где вместо  подставляют ее приближенное значение подставляют ее приближенное значение  , найденное по формуле (62). , найденное по формуле (62).
Итак, для достаточно больших значений n имеем
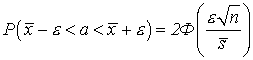
| (63)
| где

| (64)
| Интервал  называется доверительным интервалом, а вероятность называется доверительным интервалом, а вероятность  — надежностью *. — надежностью *.
Пример. Для определения процентного содержания хрома в стали были проделаны 34 измерения, результаты которых сведены в таблицу:
| №
| xi
| 
| 
| |
| 4, 505
|
|
| |
| 4, 524
| 0, 019
| 0, 000361
| |
| 4, 492
| -0, 013
| 0, 000169
| |
| 4, 5
| -0, 005
| 0, 000025
| |
| 4, 493
| -0, 012
| 0, 000144
| |
| 4, 515
| 0, 01
| 0, 0001
| |
| 4, 504
| -0, 001
| 0, 000001
| |
| 4, 508
| 0, 003
| 0, 000009
| |
| 4, 517
| 0, 012
| 0, 000144
| |
| 4, 513
| 0, 008
| 0, 000064
| |
| 4, 519
| 0, 014
| 0, 000196
| |
| 4, 511
| 0, 006
| 0, 000036
| |
| 4, 485
| -0, 02
| 0, 0004
| |
| 4, 497
| -0, 008
| 0, 000064
| |
| 4, 502
| -0, 003
| 0, 000009
| |
| 4, 507
| 0, 002
| 0, 000004
| |
| 4, 501
| -0, 004
| 0, 000016
| |
| 4, 501
| -0, 004
| 0, 000016
|
| | №
| xi
| 
| 
| |
| 4, 507
| 0, 002
| 0, 000004
| |
| 4, 502
| -0, 003
| 0, 000009
| |
| 4, 497
| -0, 008
| 0, 000064
| |
| 4, 485
| -0, 02
| 0, 0004
| |
| 4, 511
| 0, 006
| 0, 000036
| |
| 4, 519
| 0, 014
| 0, 000196
| |
| 4, 513
| 0, 008
| 0, 000064
| |
| 4, 517
| 0, 012
| 0, 000144
| |
| 4, 508
| 0, 003
| 0, 000009
| |
| 4, 504
| -0, 001
| 0, 000001
| |
| 4, 515
| 0, 01
| 0, 0001
| |
| 4, 493
| -0, 012
| 0, 000144
| |
| 4, 5
| -0, 005
| 0, 000025
| |
| 4, 492
| -0, 013
| 0, 000169
| |
| 4, 424
| 0, 019
| 0, 000361
| |
| 4, 505
|
|
| 
| 153, 186
|
| 0, 006968
|
| Найти доверительный интервал с надежностью  =0, 9973 =0, 9973
Решение:
Здесь n=34. Используя табличные данные, находим



При надежности  =0, 9973 по формуле (63) получим =0, 9973 по формуле (63) получим

Cледовательно,

Из табл. II Приложения найдем

В данном случае доверительный интервал

Итак с надежностью  =0, 9973 процентное содержание хрома в стали находится в интервале ] 4, 498; 4, 513 [. =0, 9973 процентное содержание хрома в стали находится в интервале ] 4, 498; 4, 513 [.
|
Расчет по формуле (63) дает удовлетворительные по точности результаты при  . .

Шрифт зодчего Шрифт зодчего состоит из прописных (заглавных), строчных букв и цифр...
|

Картограммы и картодиаграммы Картограммы и картодиаграммы применяются для изображения географической характеристики изучаемых явлений...
|

Практические расчеты на срез и смятие При изучении темы обратите внимание на основные расчетные предпосылки и условности расчета...
|

Функция спроса населения на данный товар Функция спроса населения на данный товар: Qd=7-Р. Функция предложения: Qs= -5+2Р,где...
|
|
Йодометрия. Характеристика метода Метод йодометрии основан на ОВ-реакциях, связанных с превращением I2 в ионы I- и обратно...
Броматометрия и бромометрия Броматометрический метод основан на окислении восстановителей броматом калия в кислой среде...
Метод Фольгарда (роданометрия или тиоцианатометрия) Метод Фольгарда основан на применении в качестве осадителя титрованного раствора, содержащего роданид-ионы SCN...
|
|
Типология суицида. Феномен суицида (самоубийство или попытка самоубийства) чаще всего связывается с представлением о психологическом кризисе личности...
ОСНОВНЫЕ ТИПЫ МОЗГА ПОЗВОНОЧНЫХ Ихтиопсидный тип мозга характерен для низших позвоночных - рыб и амфибий...
Принципы, критерии и методы оценки и аттестации персонала
Аттестация персонала является одной их важнейших функций управления персоналом...
|
|

 (i — номер измерения). Так как каждое измерение не зависит от результатов других измерений, то мы имеем n случайных независимых величин
(i — номер измерения). Так как каждое измерение не зависит от результатов других измерений, то мы имеем n случайных независимых величин  . Обозначим через x1, x2,..., xn фактически полученные результаты n измерений величины а. Таким образом, xi есть одно из возможных значений
. Обозначим через x1, x2,..., xn фактически полученные результаты n измерений величины а. Таким образом, xi есть одно из возможных значений 
 (i=1, 2,..., n). Далее будем предполагать, что все измерения проводятся с одинаковой степенью точности (равноточные измерения). Поэтому дисперсии всех случайных величин должны быть одинаковыми, т. е.
(i=1, 2,..., n). Далее будем предполагать, что все измерения проводятся с одинаковой степенью точности (равноточные измерения). Поэтому дисперсии всех случайных величин должны быть одинаковыми, т. е.  .
.  . Так как возможный результат i -гo измерения есть случайная величина
. Так как возможный результат i -гo измерения есть случайная величина  также имеет нормальное распределение с тем же математическим ожиданием
также имеет нормальное распределение с тем же математическим ожиданием  , и средним квадратическим отклонением
, и средним квадратическим отклонением  (см. § 4, п. 3). Поэтому плотность распределения вероятностей для средней арифметической
(см. § 4, п. 3). Поэтому плотность распределения вероятностей для средней арифметической  имеет вид
имеет вид 

 интервал
интервал  будет содержать а, на основании формулы (33) определяется соотношением
будет содержать а, на основании формулы (33) определяется соотношением
 и
и  . Соотношение (58) справедливо для любого значения
. Соотношение (58) справедливо для любого значения  . Вероятность
. Вероятность  не зависит от конкретных значений, которые принимают случайные величины
не зависит от конкретных значений, которые принимают случайные величины 
 . Величина
. Величина  называется средней выборочной. Формулой (59) в большинстве случаев пользоваться нельзя, так как обычно значение
называется средней выборочной. Формулой (59) в большинстве случаев пользоваться нельзя, так как обычно значение 
 , и дисперсию, равную
, и дисперсию, равную  , т.е.
, т.е. 

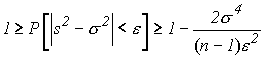
 , то
, то  , т.е. s2 стремится по вероятности к
, т.е. s2 стремится по вероятности к 
 есть одно из возможных значений s2, то при достаточно больших n с практической достоверностью можно утверждать, что имеет место приближенное равенство
есть одно из возможных значений s2, то при достаточно больших n с практической достоверностью можно утверждать, что имеет место приближенное равенство
 , пользуются формулой (59), где вместо
, пользуются формулой (59), где вместо  , найденное по формуле (62).
, найденное по формуле (62). 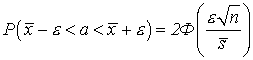

 — надежностью *.
— надежностью *.

 =0, 9973
=0, 9973






 .
.


