Пусть  и
и 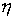 - две случайные непрерывные величины, находящиеся в корреляционной зависимости. Это значит, что каждому значению x случайной величины
- две случайные непрерывные величины, находящиеся в корреляционной зависимости. Это значит, что каждому значению x случайной величины  соответствует вполне определенное распределение вероятностей величины
соответствует вполне определенное распределение вероятностей величины 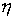 . Плотность
. Плотность  распределения величины
распределения величины 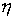 при условии, что
при условии, что 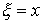 , называется условной плотностью распределения случайной величины
, называется условной плотностью распределения случайной величины 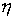 .
.
Вычислим для данного случая так называемое условное математическое ожидание  величины
величины 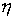 при условии, что
при условии, что 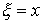 . Согласно определению математического ожидания непрерывной случайной величины, имеем
. Согласно определению математического ожидания непрерывной случайной величины, имеем

[см. формулу (40)]. Каждому возможному значению x случайной величины  соответствует определенное значение условного математического ожидания
соответствует определенное значение условного математического ожидания  . Таким образом, мы получаем функцию
. Таким образом, мы получаем функцию 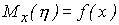 переменной x. Эта функция y=f(x) называется функцией регрессии величины
переменной x. Эта функция y=f(x) называется функцией регрессии величины 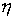 на
на  , а ее график - линией регрессии
, а ее график - линией регрессии 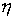 на
на  .
.
Аналогично определяется условное математическое ожидание величины  при условии, что
при условии, что  :
:

где  - условная плотность вероятности случайной величины
- условная плотность вероятности случайной величины  при условии, что
при условии, что  .
.
Функция x=g(y) называется функцией регрессии величины  на
на 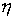 , а ее график - линией регрессии
, а ее график - линией регрессии  на
на 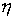 .
.
Cледует иметь в виду, что функции y=f(x) и x=g(y) не являются обратными по отношению друг к другу.
Если обе функции 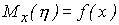 и
и  линейны, то линиями регрессии являются прямые. В этом случае говорят, что случайные величины
линейны, то линиями регрессии являются прямые. В этом случае говорят, что случайные величины  и
и 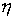 связаны линейной корреляционной зависимостью. Можно показать, что уравнение прямой регрессии
связаны линейной корреляционной зависимостью. Можно показать, что уравнение прямой регрессии 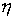 на
на  имеет следующий вид:
имеет следующий вид:

| (74)
|
где  - условное математическое ожидание случайной величины
- условное математическое ожидание случайной величины 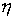 при
при 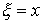 . Аналогично записывается уравнение прямой регрессии
. Аналогично записывается уравнение прямой регрессии  на
на 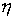 :
:
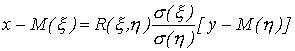
| (75)
|
где 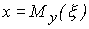 - условное математическое ожидание случайной величины
- условное математическое ожидание случайной величины  при
при  .
.
Величины
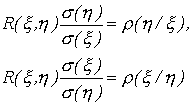
| (76)
|
называются коэффициентами регрессии соответственно 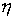 на
на  и
и  на
на 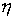 .
.
Из формул (76) следует, что

| (77)
|
Равенство (77) показывает, что оба коэффициента регрессии имеют одинаковые знаки. Если они положительны (отрицательны), то с возрастанием аргумента возрастают (убывают) соответствующие условные математические ожидания.
Если  , то, как следует из уравнений (74) и (75),
, то, как следует из уравнений (74) и (75), 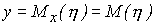 и
и  , т.е. в этом случае условные математические ожидания постоянны и равны соответствующим математическим ожиданиям случайных величин
, т.е. в этом случае условные математические ожидания постоянны и равны соответствующим математическим ожиданиям случайных величин 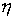 и
и  .
.
Замечание. Можно доказать, что если система двух случайных величин имеет нормальное распределение, то эти величины находятся в линейной корреляционной зависимости.

 и
и 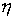 - две случайные непрерывные величины, находящиеся в корреляционной зависимости. Это значит, что каждому значению x случайной величины
- две случайные непрерывные величины, находящиеся в корреляционной зависимости. Это значит, что каждому значению x случайной величины  распределения величины
распределения величины 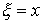 , называется условной плотностью распределения случайной величины
, называется условной плотностью распределения случайной величины  величины
величины 
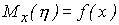 переменной x. Эта функция y=f(x) называется функцией регрессии величины
переменной x. Эта функция y=f(x) называется функцией регрессии величины  :
:
 - условная плотность вероятности случайной величины
- условная плотность вероятности случайной величины  линейны, то линиями регрессии являются прямые. В этом случае говорят, что случайные величины
линейны, то линиями регрессии являются прямые. В этом случае говорят, что случайные величины 
 - условное математическое ожидание случайной величины
- условное математическое ожидание случайной величины 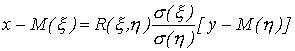
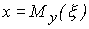 - условное математическое ожидание случайной величины
- условное математическое ожидание случайной величины 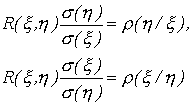

 , то, как следует из уравнений (74) и (75),
, то, как следует из уравнений (74) и (75), 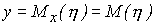 и
и  , т.е. в этом случае условные математические ожидания постоянны и равны соответствующим математическим ожиданиям случайных величин
, т.е. в этом случае условные математические ожидания постоянны и равны соответствующим математическим ожиданиям случайных величин 


