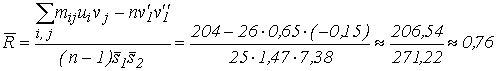Одной из задач математической статистики является исследование корреляционной зависимости между случайными величинами. Пусть проведено n опытов, в результате которых получены следующие значения системы величин 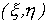 :
:
(x1, y1), (x2, y2),..., (xi, yi),..., (xn, yn).
За приближенные значения  ,
,  ,
,  и
и  принимают их выборочные значения
принимают их выборочные значения  ,
, 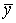 ,
,  и
и  [см. формулы (66) и (67)]:
[см. формулы (66) и (67)]:

| (78)
|
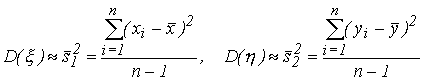
| (79)
|
Выборочными коэффициентами корреляции называют число 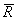 , определяемое соотношением:
, определяемое соотношением:

| (80)
|
Можно показать, что 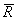 сходится по вероятности к коэффициенту корреляции
сходится по вероятности к коэффициенту корреляции  .
.
Заменяя в соотношениях (76) величины  ,
,  и
и  их выборочными значениями
их выборочными значениями  ,
,  и
и 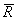 [см. формулы (79) и (80)], получим приближенные значения коэффициентов регрессии:
[см. формулы (79) и (80)], получим приближенные значения коэффициентов регрессии:
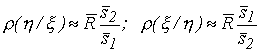
| (81)
|
Подставляя в уравнения (74) и (75) приближенные значения коэффициентов регрессии и используя соотношения (78) и (81), получим уравнения эмпирических прямых регрессий:
 на
на 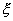 :
:

| (82)
|
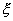 на
на  :
:

| (83)
|
При большом числе опытов для упрощения подсчета значений  ,
, 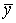 ,
,  ,
,  и коэффициента корреляции
и коэффициента корреляции 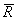 поступим следующим образом (см. § 9, п. 2, замечание).
поступим следующим образом (см. § 9, п. 2, замечание).
Диапазоны изменения наблюдаемых значений случайных величин 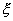 и
и  разобьем соответственно на интервалы
разобьем соответственно на интервалы
]X0, X1[, ]X1, X2[,..., ]Xi-1, Xi[,..., ]Xk-1, Xk[
и
]Y0, Y1[, ]Y1, Y2[,..., ]Yj-1, Yj[,..., ]Ys-1, Ys[
Каждое из наблюдаемых значений  , попавших в i-й (j-й) интервал, считаем приближенно равным середине этого интервала ci (dj). Пусть
, попавших в i-й (j-й) интервал, считаем приближенно равным середине этого интервала ci (dj). Пусть  (
(  ) - число значений
) - число значений  , попавших в в i-й (j-й) интервал, а x0 и y0 - произвольные числа, близкие к серединам диапазонов изменения значений
, попавших в в i-й (j-й) интервал, а x0 и y0 - произвольные числа, близкие к серединам диапазонов изменения значений 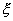 и
и  . Полагая ui=ci-x0 и vj=dj-y0 и используя формулы (70) и (71), получим:
. Полагая ui=ci-x0 и vj=dj-y0 и используя формулы (70) и (71), получим:
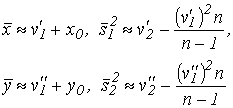
| (84)
|
где

Для подсчета выборочного коэффициента корреляции 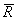 по формуле (80) сначала запишем выражение
по формуле (80) сначала запишем выражение  в новых переменных ui=ci-x0 и vj=dj-y0. Обозначим через mij число наблюдаемых значений пар
в новых переменных ui=ci-x0 и vj=dj-y0. Обозначим через mij число наблюдаемых значений пар 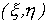 , у которых значения
, у которых значения 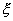 попали в i -й интервал ] Xi-1, Xi [, а значения
попали в i -й интервал ] Xi-1, Xi [, а значения  - в j -й интервал ] Yj-1, Yj [. Каждое из этих значений
- в j -й интервал ] Yj-1, Yj [. Каждое из этих значений 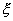 и
и  заменим соответствующими серединами ci и dj интервалов ] Xi-1, Xi [ и ] Yj-1, Yj [. Тогда
заменим соответствующими серединами ci и dj интервалов ] Xi-1, Xi [ и ] Yj-1, Yj [. Тогда

где сумма в правой части равенства распространена на все возможные пары чисел (i, j), причем i пробегает значения от 1 до k, а j - от 1 до s. После преобразований в результате получим

Итак, окончательная расчетная формула для выборочного коэффициента корреляции имеет вид
Пример. Для выяснения зависимости между диаметром ствола (  ) сосны и ее высотой (
) сосны и ее высотой ( 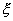 ) было исследовано 26 сосен. Наблюдаемые значения высоты сосен колеблются в границах от 22, 5 до 28, 5 м, диаметр ствола - от 20 до 48 см. Разбивая диапазон изменения высоты сосны на интервалы длиной 1 м, а диапазон изменения диаметра ствола на интервалы длиной 4 см, получим таблицу, приведенную вразделе 9.1.
) было исследовано 26 сосен. Наблюдаемые значения высоты сосен колеблются в границах от 22, 5 до 28, 5 м, диаметр ствола - от 20 до 48 см. Разбивая диапазон изменения высоты сосны на интервалы длиной 1 м, а диапазон изменения диаметра ствола на интервалы длиной 4 см, получим таблицу, приведенную вразделе 9.1.
Эта таблица называется корреляционной. В каждой ее клетке стоит число сосен, диаметр ствола и высота которых находится в указанных границах (числа
mij). При подсчете статистических характеристик примем высоту всех сосен, попавших в данный интервал, равной середине
сi этого интервала, а диаметр ствола - равным середине
dj cоответствующего интервала. Подсчет выборочных средних, дисперсий и коэффициента корреляции производим по формулам (84) и (85). Для подсчета

,
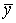
,

и

составляем две вспомогательные таблицы, принимая
x0=25 и
y0=34, т.е.
ui=ci-25 и
vj=dj-34.
Из первой таблицы для высоты сосны 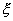 получаем
получаем



Из второй таблицы для диаметра ствола сосны  находим
находим



Для подсчета  составляем новую таблицу. В каждой ее клетке (справа) указано число mij сосен, имеющих одни и те же значения ui а vj, а слева указано произведение mijuivj. Последний столбец состоит из суммы всех mijuivj при постоянном j. Как видно из таблицы
составляем новую таблицу. В каждой ее клетке (справа) указано число mij сосен, имеющих одни и те же значения ui а vj, а слева указано произведение mijuivj. Последний столбец состоит из суммы всех mijuivj при постоянном j. Как видно из таблицы 
|
| ui
|
|
| vj
| -2
| -1
|
|
|
|
| 
|
| -12
| 48 \ 2
|
|
|
|
|
|
|
| -8
|
| 16 \ 2
| 0 \ 1
| -16 \ 2
|
|
|
|
| -4
|
| 8 \ 2
| 0 \ 2
|
| -8 \ 1
|
|
|
|
|
|
| 0 \ 2
| 0 \ 1
|
|
|
|
|
|
|
| 0 \ 1
| 4 \ 1
| 16 \ 2
|
|
|
|
|
|
|
| 16 \ 2
|
| 72 \ 3
|
|
|
|
|
|
|
| 48 \ 2
|
|
|
|
|
|
|
|
|
|
|
|
Используя формулу (85), найдем выборочный коэффициент корреляции:
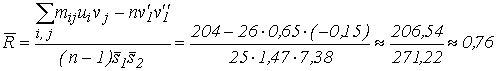
По формулам (81) находим приближенные значения коэффициентов регрессии:


По формулам (82) и (83) найдем эмпирические уравнения прямых регрессий.
Уравнение прямой регрессии  на
на 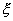 имеет вид
имеет вид
y-33, 85=3, 81(x-25, 65), или y=3, 81x-63, 88
Это уравнение дает зависимость среднего значения диаметра ствола от его длины.
Уравнение прямой регрессии 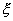 на
на  имеет вид
имеет вид
x-25, 65=0, 15(y-33, 85), или x=0, 15y+21, 57
Последнее уравнение дает зависимость среднего значения длины ствола от его диаметра.
 ,
, 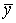 ,
,  и
и  составляем две вспомогательные таблицы, принимая x0=25 и y0=34, т.е. ui=ci-25 и vj=dj-34.
составляем две вспомогательные таблицы, принимая x0=25 и y0=34, т.е. ui=ci-25 и vj=dj-34. 
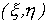 :
: ,
,  ,
,  и
и  принимают их выборочные значения
принимают их выборочные значения  и
и  [см. формулы (66) и (67)]:
[см. формулы (66) и (67)]:
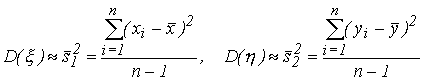
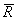 , определяемое соотношением:
, определяемое соотношением:
 .
.  ,
,  и
и 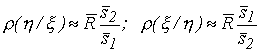
 на
на 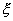 :
:

 , попавших в i-й (j-й) интервал, считаем приближенно равным середине этого интервала ci (dj). Пусть
, попавших в i-й (j-й) интервал, считаем приближенно равным середине этого интервала ci (dj). Пусть  (
(  ) - число значений
) - число значений 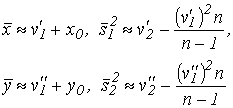

 в новых переменных ui=ci-x0 и vj=dj-y0. Обозначим через mij число наблюдаемых значений пар
в новых переменных ui=ci-x0 и vj=dj-y0. Обозначим через mij число наблюдаемых значений пар 











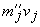







 составляем новую таблицу. В каждой ее клетке (справа) указано число mij сосен, имеющих одни и те же значения ui а vj, а слева указано произведение mijuivj. Последний столбец состоит из суммы всех mijuivj при постоянном j. Как видно из таблицы
составляем новую таблицу. В каждой ее клетке (справа) указано число mij сосен, имеющих одни и те же значения ui а vj, а слева указано произведение mijuivj. Последний столбец состоит из суммы всех mijuivj при постоянном j. Как видно из таблицы