Имеет место следующее утверждение. Пусть  - последовательность попарно независимых случайных величин, имеющих ограниченные в совокупности дисперсии, т. е.
- последовательность попарно независимых случайных величин, имеющих ограниченные в совокупности дисперсии, т. е.  для любого i. Тогда, каково бы нибыло
для любого i. Тогда, каково бы нибыло  , справедливо соотношение
, справедливо соотношение

| (54)
|
Доказательство:
Обозначим через  величину
величину 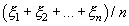 , т.е. среднюю арифметическую n случайных величин. Случайная величина
, т.е. среднюю арифметическую n случайных величин. Случайная величина  имеет математическое ожидание
имеет математическое ожидание

и дисперсию

(здесь мы воспользовались свойствами математического ожидания и дисперсии). Применяя к случайной величине  вторую лемму Чебышева, найдем, что
вторую лемму Чебышева, найдем, что

т.е.

так как  при любом i, и следовательно,
при любом i, и следовательно,

Учитывая, что вероятность любого события не превосходит единицы, получим

Переходя к пределу при  , имеем
, имеем

Смысл закона больших чисел Чебышева состоит в следующем. В то время как отдельная случайная величина может принимать значения, очень далекие от своего математического ожидания, средняя арифметическая большого числа случайных величин с вероятностью, близкой к единице, принимает значение, мало отличающееся от среднего арифметического их математических ожиданий.
Частный случай закона больших чисел Чебышева. Пусть  - последовательность попарно независимых случайных величин, имеющих ограниченные в совокупности дисперсии, т. е.
- последовательность попарно независимых случайных величин, имеющих ограниченные в совокупности дисперсии, т. е.  и одинаковые математические ожидания
и одинаковые математические ожидания 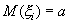 . Тогда, каково бы нибыло
. Тогда, каково бы нибыло  , справедливо соотношение
, справедливо соотношение

Это непосредственно следует из формулы (54), так как

Замечание. Говорят, что случайная величина 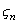 сходится по вероятности к числу А, если при сколь угодно малом
сходится по вероятности к числу А, если при сколь угодно малом  вероятность неравенства
вероятность неравенства 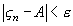 с увеличением n неограниченно приближается к единице. Сходимость по вероятности не означает, что
с увеличением n неограниченно приближается к единице. Сходимость по вероятности не означает, что  . Действительно, в последнем случае неравенство
. Действительно, в последнем случае неравенство 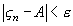 выполняется для всех достаточно больших значений n. В случае же сходимости по вероятности это неравенство для отдельных сколь угодно больших значений n может не выполняться. Однако невыполнение неравенства
выполняется для всех достаточно больших значений n. В случае же сходимости по вероятности это неравенство для отдельных сколь угодно больших значений n может не выполняться. Однако невыполнение неравенства 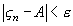 для больших значений n есть событие очень редкое (маловероятное). Принимая это во внимание, частный случай закона больших чисел Чебышева можно сформулировать так.
для больших значений n есть событие очень редкое (маловероятное). Принимая это во внимание, частный случай закона больших чисел Чебышева можно сформулировать так.
Средняя арифметическая 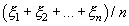 попарно независимых случайных величин
попарно независимых случайных величин  , имеющих ограниченные в совокупности дисперсии и одинаковые математические ожидания
, имеющих ограниченные в совокупности дисперсии и одинаковые математические ожидания 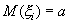 , сходится по вероятности к а.
, сходится по вероятности к а.
Поясним смысл частного случая закона больших чисел Чебышева. Пусть требуется найти истинное значение а некоторой физической величины (например, размер некоторой детали). Для этого будем производить ряд независимых друг от друга измерений. Всякое измерение сопровождается некоторой погрешностью (см. подробнее § 6, п. 1). Поэтому каждый возможный результат измерения есть случайная величина  (индекс i — номер измерения). Предположим, что в каждом измерении нет систематической ошибки, т. е. отклонения от истинного значения а измеряемой величины в ту и другую стороны равновероятны. В этом случае математические ожидания всех случайных величин
(индекс i — номер измерения). Предположим, что в каждом измерении нет систематической ошибки, т. е. отклонения от истинного значения а измеряемой величины в ту и другую стороны равновероятны. В этом случае математические ожидания всех случайных величин  одинаковы и равны измеряемой величине а, т. е.
одинаковы и равны измеряемой величине а, т. е. 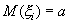
Предположим, наконец, что измерения производятся с некоторой гарантированной точностью. Это значит, что для всех измерений  . Таким образом, мы находимся в условиях закона больших чисел Чебышева, а потому, если число измерений достаточно велико, то с практической достоверностью можно утверждать, что каково бы ни было
. Таким образом, мы находимся в условиях закона больших чисел Чебышева, а потому, если число измерений достаточно велико, то с практической достоверностью можно утверждать, что каково бы ни было  , средняя арифметическая результатов измерений отличается от истинного значения а меньше, чем на
, средняя арифметическая результатов измерений отличается от истинного значения а меньше, чем на 

 - последовательность попарно независимых случайных величин, имеющих ограниченные в совокупности дисперсии, т. е.
- последовательность попарно независимых случайных величин, имеющих ограниченные в совокупности дисперсии, т. е.  для любого i. Тогда, каково бы нибыло
для любого i. Тогда, каково бы нибыло  , справедливо соотношение
, справедливо соотношение
 величину
величину 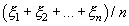 , т.е. среднюю арифметическую n случайных величин. Случайная величина
, т.е. среднюю арифметическую n случайных величин. Случайная величина 

 вторую лемму Чебышева, найдем, что
вторую лемму Чебышева, найдем, что 



 , имеем
, имеем 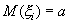 . Тогда, каково бы нибыло
. Тогда, каково бы нибыло 

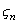 сходится по вероятности к числу А, если при сколь угодно малом
сходится по вероятности к числу А, если при сколь угодно малом 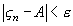 с увеличением n неограниченно приближается к единице. Сходимость по вероятности не означает, что
с увеличением n неограниченно приближается к единице. Сходимость по вероятности не означает, что  . Действительно, в последнем случае неравенство
. Действительно, в последнем случае неравенство  , имеющих ограниченные в совокупности дисперсии и одинаковые математические ожидания
, имеющих ограниченные в совокупности дисперсии и одинаковые математические ожидания  (индекс i — номер измерения). Предположим, что в каждом измерении нет систематической ошибки, т. е. отклонения от истинного значения а измеряемой величины в ту и другую стороны равновероятны. В этом случае математические ожидания всех случайных величин
(индекс i — номер измерения). Предположим, что в каждом измерении нет систематической ошибки, т. е. отклонения от истинного значения а измеряемой величины в ту и другую стороны равновероятны. В этом случае математические ожидания всех случайных величин 



