Пусть мы имеем дело с непрерывной случайной величиной 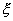 , значения которой получены из наблюдений. Разобьем диапазон наблюдаемых значений
, значения которой получены из наблюдений. Разобьем диапазон наблюдаемых значений 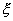 на интервалы ] X0, X1 [, ] X1, X2 [,..., ] Xk-1, Xk [ одинаковой длины
на интервалы ] X0, X1 [, ] X1, X2 [,..., ] Xk-1, Xk [ одинаковой длины 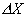 . Пусть mi - число наблюдаемых значений
. Пусть mi - число наблюдаемых значений 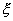 , попавших в i -й интервал. Разделив mi на общее число наблюдений n, получим частоту
, попавших в i -й интервал. Разделив mi на общее число наблюдений n, получим частоту  , соответствующую i -му интервалу:
, соответствующую i -му интервалу:  , причем
, причем  . Составим следующую таблицу:
. Составим следующую таблицу:
| Номер интервала
| Интервал
| mi
| 
|
|
| ] X0, X1 [
| m1
| 
|
|
| ] X1, X2 [
| m2
| 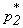
|
| ...
| ...
| ...
| ...
|
| k
| ] Xk-1, Xk [
| mk
| 
|
которая называется статистическим рядом. Эмпирической (или статистической) функцией распределения случайной величины 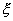 называется частота события, заключающегося в том, что величина
называется частота события, заключающегося в том, что величина 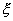 в результате опыта примет значение, меньшее x:
в результате опыта примет значение, меньшее x:

На практике достаточно найти значения статистической функции распределения F*(x) в точках X0, X1,..., Xk, которые являются границами интервалов статистического ряда:

| (65)
|
Cледует заметить, что F*(x)=0 при x< X0 и F*(x)=1 при x> Xk. Построив точки Mi [Xi; F*(Xi)] и соединив их плавной кривой, получим приближенный график эмпирической функции распределения (рис. 15). Используя закон больших чисел Бернулли, можно доказать, что при достаточно большом числе n испытаний с вероятностью, близкой к единице, эмпирическая функция распределения F*(x) отличается сколь угодно мало от неизвестной нам функции распределения F(x) cлучайной величины 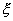


Часто вместо построения графика эмпирической функции распределения поступают следующим образом. На оси абсцисс откладывают интервалы ] X0, X1 [, ] X1, X2 [,..., ] Xk-1, Xk [. На каждом интервале строят прямоугольник, площадь которого равна частоте  , соответствующей данному интервалу. Высота hi этого прямоугольника равна
, соответствующей данному интервалу. Высота hi этого прямоугольника равна 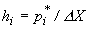 , где
, где 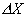 - длинна каждого из интервалов. Ясно, что сумма площадей всех построенных прямоугольников равна единице.
- длинна каждого из интервалов. Ясно, что сумма площадей всех построенных прямоугольников равна единице.
Рассмотрим функцию  , которая в интервале ] Xi-1, Xi [ постоянна и равна hi. График этой функции называется гистограммой. Он представляет собой ступенчатую линию (рис. 16). С помощью закона больших чисел Бернулли можно доказать, что при малых
, которая в интервале ] Xi-1, Xi [ постоянна и равна hi. График этой функции называется гистограммой. Он представляет собой ступенчатую линию (рис. 16). С помощью закона больших чисел Бернулли можно доказать, что при малых 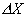 и больших n с практической достоверностью
и больших n с практической достоверностью  как угодно мало отличается от плотности распределения
как угодно мало отличается от плотности распределения  непрерывной случайной величины
непрерывной случайной величины 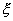 .
.
Пример. Измерен диаметр у 270 валов хвостовика. Значения диаметра (в см) оказались в диапазоне 66-90 см. Разбив этот диапазон на интервалы диной 2 см ( 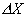 =2), получим статистический ряд (см. таблицу)
=2), получим статистический ряд (см. таблицу)
| Номера интервалов
| Интервалы
| mi
| 
| 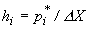
|
| (1)
| (2)
| (3)
| (4)
| (5)
|
|
| ]66, 68[
|
| 0, 015
| 0, 008
|
|
| ]68, 70[
|
| 0, 045
| 0, 022
|
|
| ]70, 72[
|
| 0, 090
| 0, 045
|
|
| ]72, 74[
|
| 0, 152
| 0, 076
|
|
| ]74, 76[
|
| 0, 185
| 0, 092
|
|
| ]76, 78[
|
| 0, 196
| 0, 098
|
|
| ]78, 80[
|
| 0, 144
| 0, 072
|
|
| ]80, 82[
|
| 0, 096
| 0, 048
|
|
| ]82, 84[
|
| 0, 048
| 0, 024
|
|
| ]84, 86[
|
| 0, 019
| 0, 009
|
|
| ]86, 88[
|
| 0, 007
| 0, 004
|
|
| ]88, 90[
|
| 0, 003
| 0, 002
|

|
|
| 1, 000
|
|
Построим гистограмму и эмпирическую функцию распределения. Подсчитанные частоты  приведены в столбце (4), а значения высот hi прямоугольников гистограммы - в столбце (5). Гистограмма изображена на рис. 17.
приведены в столбце (4), а значения высот hi прямоугольников гистограммы - в столбце (5). Гистограмма изображена на рис. 17.


Значения эмпирической функции распределения в граничных точках интервалов вычислены по формуле (65) и приведены в следующей таблице:
| x
|
|
|
|
|
|
|
|
|
|
|
|
|
|
| F*(x)
|
| 0, 015
| 0, 060
| 0, 150
| 0, 302
| 0, 487
| 0, 683
| 0, 827
| 0, 923
| 0, 971
| 0, 990
| 0, 997
| 1, 000
|
Так, например,

График функции F*(x) изображен на рис.18.

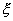 , значения которой получены из наблюдений. Разобьем диапазон наблюдаемых значений
, значения которой получены из наблюдений. Разобьем диапазон наблюдаемых значений 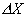 . Пусть mi - число наблюдаемых значений
. Пусть mi - число наблюдаемых значений  , соответствующую i -му интервалу:
, соответствующую i -му интервалу:  , причем
, причем  . Составим следующую таблицу:
. Составим следующую таблицу:
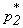





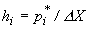 , где
, где  , которая в интервале ] Xi-1, Xi [ постоянна и равна hi. График этой функции называется гистограммой. Он представляет собой ступенчатую линию (рис. 16). С помощью закона больших чисел Бернулли можно доказать, что при малых
, которая в интервале ] Xi-1, Xi [ постоянна и равна hi. График этой функции называется гистограммой. Он представляет собой ступенчатую линию (рис. 16). С помощью закона больших чисел Бернулли можно доказать, что при малых  как угодно мало отличается от плотности распределения
как угодно мало отличается от плотности распределения  непрерывной случайной величины
непрерывной случайной величины 






