Глава 5. ЭЛЕМЕНТЫ ОПЕРАЦИОННОГО ИСЧИСЛЕНИЯ
Основными понятиями операционного исчисления являются понятия функции-оригинала и функции-изображения.
Пусть задана функция 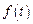 действительного переменного t. Функция действительного переменного t. Функция 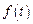 называется оригиналом или начальной функцией, если она удовлетворяет следующим условиям:
1. называется оригиналом или начальной функцией, если она удовлетворяет следующим условиям:
1.  при при  .
2. .
2. 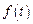 – кусочно-непрерывна при – кусочно-непрерывна при  , т.е. она непрерывна или имеет точки разрыва I рода, причем на каждом конечном промежутке таких точек лишь конечное число.
3. Существуют такие числа , т.е. она непрерывна или имеет точки разрыва I рода, причем на каждом конечном промежутке таких точек лишь конечное число.
3. Существуют такие числа  и и  , что при всех t выполняется неравенство , что при всех t выполняется неравенство  , т.е. с ростом t функция , т.е. с ростом t функция 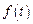 может возрастать не быстрее некоторой показательной функции. Число может возрастать не быстрее некоторой показательной функции. Число  называется показателем роста функции называется показателем роста функции 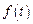 . .
|
Заметим, что функция 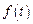 может быть и комплексной функцией действительного переменного, т.е. иметь вид
может быть и комплексной функцией действительного переменного, т.е. иметь вид  ; она считается оригиналом, если действительные функции
; она считается оригиналом, если действительные функции  и
и  являются оригиналами.
являются оригиналами.
Пусть 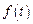 – оригинал, а
– оригинал, а 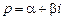 – комплексный параметр, причем
– комплексный параметр, причем  . Рассмотрим произведение функции
. Рассмотрим произведение функции 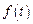 на комплексную функцию
на комплексную функцию  действительного переменного t:
действительного переменного t:  и определим несобственный интеграл
и определим несобственный интеграл
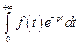 .
.
Можно показать, что при сформулированных условиях этот интеграл сходится и является функцией переменного р:
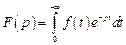 . .
|
Этот интеграл называется интегралом Лапласа, а определяемая им функция  – преобразованием Лапласа, или лапласовым изображением
– преобразованием Лапласа, или лапласовым изображением 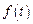 , или просто изображением
, или просто изображением 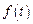 . Соответствие между оригиналом
. Соответствие между оригиналом 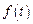 и его изображением
и его изображением  будем записывать в виде
будем записывать в виде
 или
или  .
.
Теорема (о единственности оригинала). Если две непрерывные функции 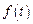 и
и 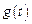 имеют одно и то же изображение
имеют одно и то же изображение  , то эти функции совпадают.
, то эти функции совпадают.

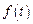 действительного переменного t. Функция
действительного переменного t. Функция  при
при  .
2.
.
2.  , т.е. она непрерывна или имеет точки разрыва I рода, причем на каждом конечном промежутке таких точек лишь конечное число.
3. Существуют такие числа
, т.е. она непрерывна или имеет точки разрыва I рода, причем на каждом конечном промежутке таких точек лишь конечное число.
3. Существуют такие числа  и
и  , что при всех t выполняется неравенство
, что при всех t выполняется неравенство  , т.е. с ростом t функция
, т.е. с ростом t функция  называется показателем роста функции
называется показателем роста функции  ; она считается оригиналом, если действительные функции
; она считается оригиналом, если действительные функции  и
и  являются оригиналами.
являются оригиналами.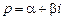 – комплексный параметр, причем
– комплексный параметр, причем  . Рассмотрим произведение функции
. Рассмотрим произведение функции  действительного переменного t:
действительного переменного t:  и определим несобственный интеграл
и определим несобственный интеграл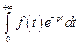 .
.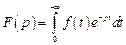 .
.
 – преобразованием Лапласа, или лапласовым изображением
– преобразованием Лапласа, или лапласовым изображением  или
или  .
.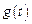 имеют одно и то же изображение
имеют одно и то же изображение 


