Теорема об интегрировании изображения
Пример. Найти изображение функций Решение. Так как
Найдем изображение для функции
Дифференцирование оригинала
Таблица некоторых изображений
Для удобства использования полученных выше изображений поместим их в одну таблицу.
Кроме того, рассмотренные выше свойства преобразований Лапласа представляют собой основные правила операционного исчисления. Для удобства использования перечислим их еще раз. 1. Линейность: 2. Подобие: 3. Смещение изображения: 4. Дифференцирование изображения: 5. Запаздывание оригинала: 6. Умножение изображений: 7. Интегрирование оригинала: 8. Интегрирование изображения: 9. Дифференцирование оригинала:
……………………………
|
и интеграл 
сходится, то 
, т.е. интегрированию изображения соответствует деление его оригинала на t.
и 
.
, то, учитывая сформулированную теорему,
.
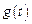, используя свойство интегрирования оригинала:
.
, 
, …, 
являются оригиналами, то
,
,
……………………………
.
.
.
.
.
.
.
.
.
.
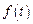
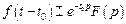