Примеры. 1. Используя операционное исчисление, найти частное решение дифференциального уравнения , удовлетворяющее начальному условию
1. Используя операционное исчисление, найти частное решение дифференциального уравнения Решение. Пусть
Выразим из полученного уравнения функцию
Представим эту рациональную дробь как сумму простейших дробей:
Итак,
2. Найти частное решение дифференциального уравнения Решение. Пусть
и Подставляя эти выражения в дифференциальное уравнение, получаем операторное уравнение:
или
Методом неопределенных коэффициентов найдем разложение этой дроби в сумму простейших дробей.
Решение. Пусть
Тогда
Операторное уравнение принимает вид
Находим из него неизвестное изображение
Разложим дробь
(При разложении можно использовать метод неопределенных коэффициентов.) Следовательно,
Еще раз используя теорему запаздывания, найдем искомое решение дифференциального уравнения:
или
4. Операционным методом решить систему линейных дифференциальных уравнений
Решение. Пусть
Получили систему линейных алгебраических уравнений относительно изображений
Итак,
Тогда
Следовательно, Таким образом, решением системы дифференциальных уравнений, удовлетворяющим заданным начальным условиям являются функции 5. Операционным методом решить систему линейных дифференциальных уравнений
Решение. Перейдем к изображениям искомых функций:
Кроме того,
Тогда система операторных уравнений будет иметь вид
или
Решим полученную систему методом Крамера.
Выпишем изображения искомых функций:
Используя метод неопределенных коэффициентов, восстановим оригиналы.
Таким образом, решением системы уравнений являются функции
Задачи для практических занятий и самостоятельной работы по теме Операционное исчисление»
1. Найдите изображения следующих функций: 1) 2) 3) Ответ: 4) 5) 6) 7) 8) 9) Ответ: 10) Ответ: 11) Ответ: 12) 13) 14) 15) 16)
2. Найдите оригиналы по заданным изображениям: 1) 2) 3) Ответ: 4) 5) 6) Ответ: 7) 8) 9) 10) 11) 12) Ответ: 13) Ответ: 14) 15) Ответ: 16)
3. Найдите свертку функций и ее изображение: 1) Ответ: 2) Ответ: 3) Ответ:
4) Ответ: 5) Ответ:
4. Найдите оригиналы для следующих изображений, используя теорему свертывания: 1) 2) 3) 4)
5. Используя теорему запаздывания, найдите изображения следующих функций:
3)
Ответ:
4)
5) 6) Ответ:
6. Используя теорему запаздывания, найдите оригиналы для следующих изображений: 1) 2) 3) Ответ: 4) Ответ:
7. Решите дифференциальные уравнения операционным методом: 1) 2) 3) 4) 5) Ответ: 6) Ответ: 7) Ответ: 8) Ответ: 9) Ответ: 10) Ответ: 11) Ответ: 12) Ответ: 13) Ответ: 14) Ответ: 15) Ответ:
16) Ответ: 17) Ответ: 18) Ответ:
8. Решите системы дифференциальных уравнений операционным методом: 1) 2) 3) Ответ: 4) Ответ: 5) Ответ: 6) Ответ: 7) Ответ: 8) Ответ: 9) Ответ: 10) Ответ: 11) Ответ:
|

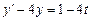 , удовлетворяющее начальному условию
, удовлетворяющее начальному условию 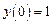 .
.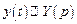 , тогда
, тогда 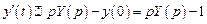 , кроме того
, кроме того 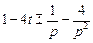 . Таким образом, применяя преобразование Лапласа к обеим частям уравнения, приходим к операторному уравнению
. Таким образом, применяя преобразование Лапласа к обеим частям уравнения, приходим к операторному уравнению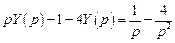 .
.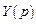 :
: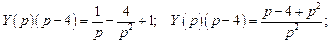
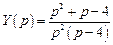 .
.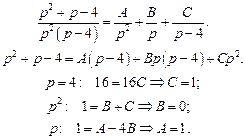
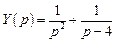 . Следовательно, решением заданного дифференциального уравнения будет функция, которая является оригиналом для полученного изображения:
. Следовательно, решением заданного дифференциального уравнения будет функция, которая является оригиналом для полученного изображения: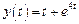 .
.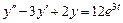 , удовлетворяющее начальным условиям
, удовлетворяющее начальным условиям 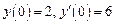 .
.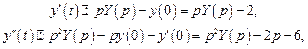
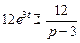 .
.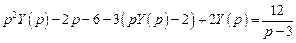 ,
,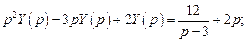
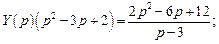
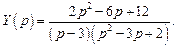
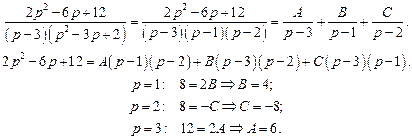 Таким образом,
Таким образом, 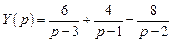 . Следовательно, частное решение данного дифференциального уравнения будет
. Следовательно, частное решение данного дифференциального уравнения будет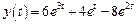 .
.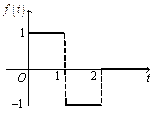 3. Решить задачу Коши
3. Решить задачу Коши 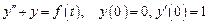 , где функция
, где функция 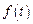 задана графически на рисунке.
задана графически на рисунке.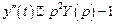 . Найдем изображение функции
. Найдем изображение функции 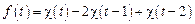 .
.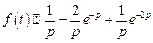 .
.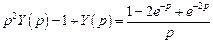 .
.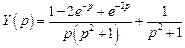 .
. в сумму простейших дробей.
в сумму простейших дробей.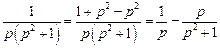 .
.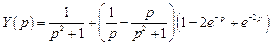 .
.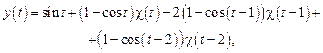
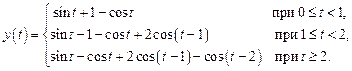

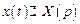 ,
,  ,
, 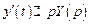 и
и  . Система операторных уравнений принимает вид
. Система операторных уравнений принимает вид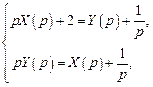 или
или 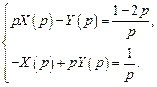
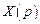 и
и  ,
,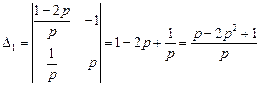 ,
,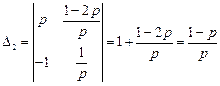 .
.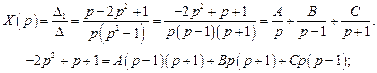
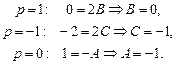
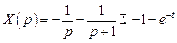 .
.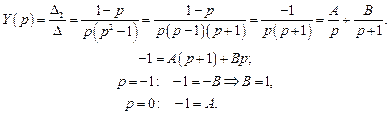
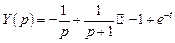 .
. ,
,  .
.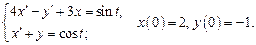
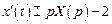 ,
, 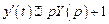 .
.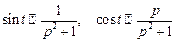 .
.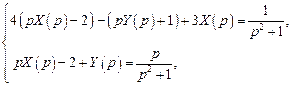
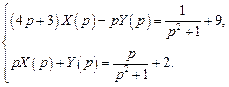
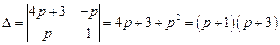 ,
,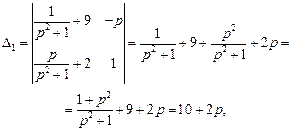

 ,
,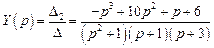 .
.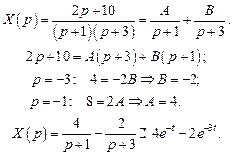
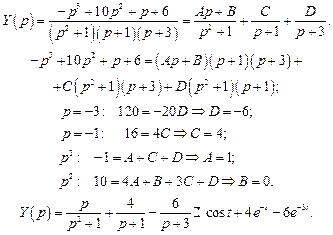
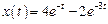 ,
, 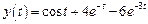 .
.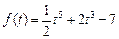 . Ответ:
. Ответ: 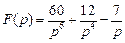 .
.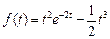 . Ответ:
. Ответ:  .
. .
.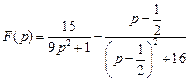 .
. . Ответ:
. Ответ:  .
.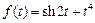 . Ответ:
. Ответ: 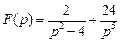 .
.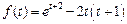 . Ответ:
. Ответ: 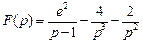 .
. . Ответ:
. Ответ: 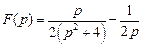 .
.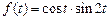 . Ответ:
. Ответ: 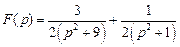 .
.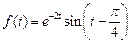 .
.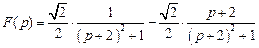 .
.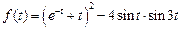 .
. .
.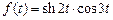 .
.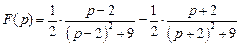 .
. . Ответ:
. Ответ: 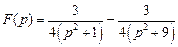 .
. . Ответ:
. Ответ: 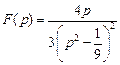 .
.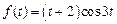 . Ответ:
. Ответ: 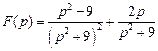 .
. . Ответ:
. Ответ: 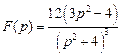 .
.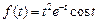 . Ответ:
. Ответ: 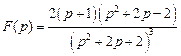 .
.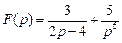 . Ответ:
. Ответ:  .
.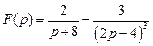 . Ответ:
. Ответ: 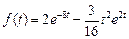 .
.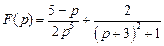 .
.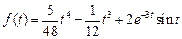 .
.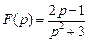 . Ответ:
. Ответ: 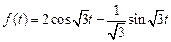 .
. . Ответ:
. Ответ: 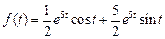 .
. .
.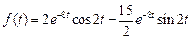 .
.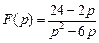 . Ответ:
. Ответ:  .
.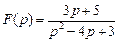 . Ответ:
. Ответ: 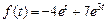 .
.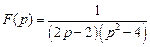 . Ответ:
. Ответ:  .
.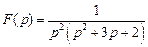 . Ответ:
. Ответ: 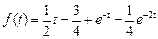 .
.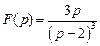 . Ответ:
. Ответ: 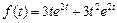 .
. .
.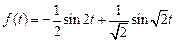 .
.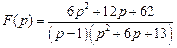 .
.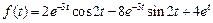 .
.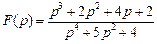 . Ответ:
. Ответ:  .
.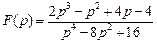 .
. .
.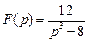 . Ответ:
. Ответ: 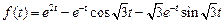 .
.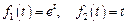 .
.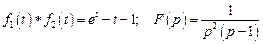 .
.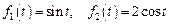 .
.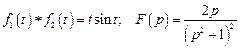 .
.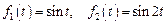 .
.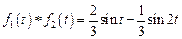 ;
;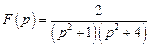 .
.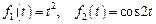 .
.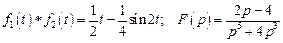 .
.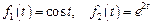 .
. ;
;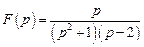 .
.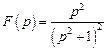 . Ответ:
. Ответ: 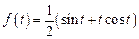 .
.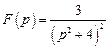 . Ответ:
. Ответ:  .
.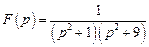 . Ответ:
. Ответ: 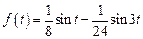 .
.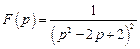 . Ответ:
. Ответ: 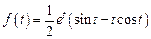 .
. 1)
1) Ответ:
Ответ: 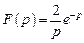 .
.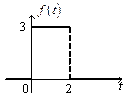 2)
2) Ответ:
Ответ: 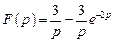 .
.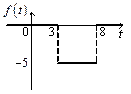
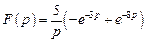 .
.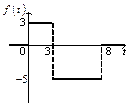
 Ответ:
Ответ: 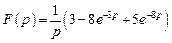 .
.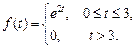 Ответ:
Ответ:  .
.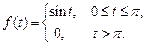
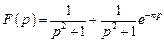 .
.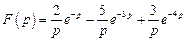 . Ответ:
. Ответ: 
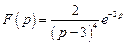 . Ответ:
. Ответ: 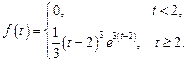
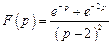 .
.
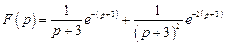 .
.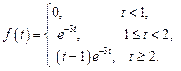
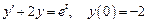 . Ответ:
. Ответ: 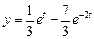 .
.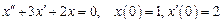 . Ответ:
. Ответ: 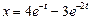 .
. . Ответ:
. Ответ: 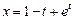 .
.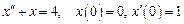 . Ответ:
. Ответ: 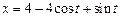 .
.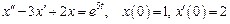 .
.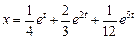 .
. .
.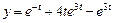 .
.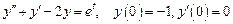 .
.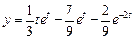 .
.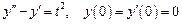 .
.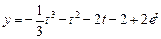 .
.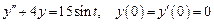 .
.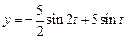 .
.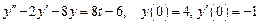 .
.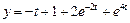 .
.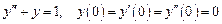 .
.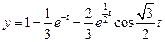 .
. .
. .
.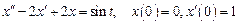 .
.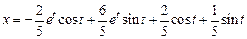 .
.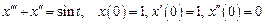 .
.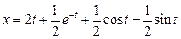 .
. .
. .
.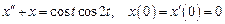 .
.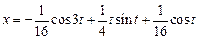 .
. , где
, где 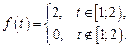
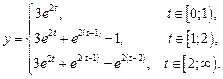
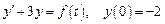 , где
, где 
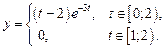
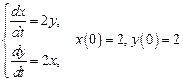 . Ответ:
. Ответ: 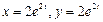 .
. Ответ:
Ответ: 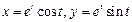 .
.
 .
.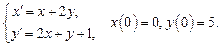
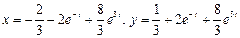 .
.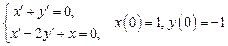 .
.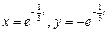 .
.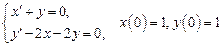 .
.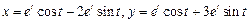 .
.
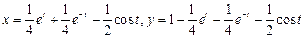 .
.
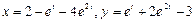 .
.
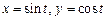 .
.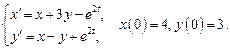
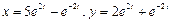 .
.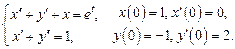
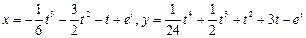 .
.


