Изображение суммы нескольких функций, умноженных на постоянные, равняется сумме изображений этих функций, умноженных на соответствующие постоянные, т.е. если 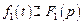 и и  , то , то
 ,
где ,
где  и и 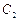 – постоянные. – постоянные.
|
Используя сформулированное свойство и выведенные соответствия  ,
, 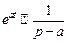 , найдем изображения функций: С,
, найдем изображения функций: С,  ,
,  ,
,  ,
,  .
.
1) 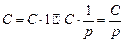 .
.
2) 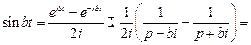
 .
.
Таким образом,  .
.
3) Аналогично, учитывая формулу  , можно доказать соответствие
, можно доказать соответствие  .
.
4) Используя определение гиперболического синуса  и свойство линейности изображения, несложно получить соответствие
и свойство линейности изображения, несложно получить соответствие  .
.
5) Аналогично из определения гиперболического косинуса  следует формула
следует формула  .
.
Свойство подобия
Если  и λ – произвольная положительная постоянная, то и λ – произвольная положительная постоянная, то  , т.е. умножение аргумента оригинала на положительное число приводит к делению изображения и его аргумента на это число. , т.е. умножение аргумента оригинала на положительное число приводит к делению изображения и его аргумента на это число.
|

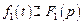 и
и  , то
, то
 ,
где
,
где  и
и 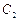 – постоянные.
– постоянные.
 ,
, 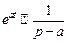 , найдем изображения функций: С,
, найдем изображения функций: С,  ,
,  ,
,  ,
,  .
.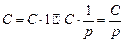 .
.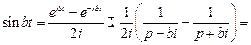
 .
. .
. , можно доказать соответствие
, можно доказать соответствие  .
. и свойство линейности изображения, несложно получить соответствие
и свойство линейности изображения, несложно получить соответствие  .
. следует формула
следует формула  .
. и λ – произвольная положительная постоянная, то
и λ – произвольная положительная постоянная, то  , т.е. умножение аргумента оригинала на положительное число приводит к делению изображения и его аргумента на это число.
, т.е. умножение аргумента оригинала на положительное число приводит к делению изображения и его аргумента на это число.



