Применение операционного исчисления к решению линейных дифференциальных уравнений и их систем
Операционный метод позволяет просто решать линейные дифференциальные уравнения с постоянными коэффициентами, в правых частях которых стоят оригиналы. Оператор Лапласа применяется к обеим частям такого уравнения, после чего получается линейное алгебраическое уравнение относительно изображения неизвестной функции. Пусть требуется найти частное решение линейного дифференциального уравнения, например, второго порядка с постоянными коэффициентами:
удовлетворяющее начальным условиям
(Для уравнений более высоких порядков решение аналогично.) Будем считать, что искомая функция
Далее, пусть для правой части уравнения
Это уравнение является линейным уравнением относительно неизвестной функции
Наконец по изображению Аналогично применяется операционный метод для решения систем линейных дифференциальных уравнений с постоянными коэффициентами.
|
,
.
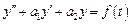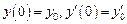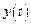вместе с ее производными и функция 
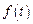являются оригиналами. Пусть 
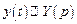. Используя теорему о дифференцировании оригинала, находим изображения производных, входящих в уравнение:
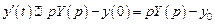и
.
и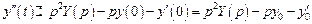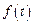зображением будет 
. Тогда, применяя преобразование Лапласа к обеим частям уравнения и пользуясь свойством линейности изображения, получим операторное (или изображающее) уравнение: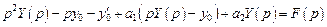
.
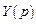. Из него находим
.
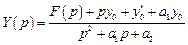