Востребованность моделей
Несколько слов о востребованности моделей. Их создание нужно не само по себе, а обусловлено необходимостью решения практических задач. Иногда решение лежит на поверхности, но если задача не востребована практикой, то и нет модели (открытия обычно рождаются тогда, когда они вызваны необходимостью, когда человечество не может сделать без них свой очередной шаг на пути прогресса). Хороший исторический пример - модель полета ракеты [15]. Дифференциальное уравнение, реализующее эту модель, принадлежит к самым простым во всей математике; оно могло быть исследовано уже вскоре после открытия Ньютоном производных – могло быть решено, скажем, в 1670 году. Однако эта модель в то время не была востребована – никому не приходило в голову применять только что разработанный математический аппарат к полету запускаемых фейерверков. И только 230 лет спустя, в 1903 году Циолковский опубликовал первое математическое исследование ракетного движения. Рассмотрим, как была выведена известная формула Циолковского. В качестве исходного для построения модели Циолковский рассматривал закон сохранения количества движения (следствие второго закона Ньютона). Если система состоит из нескольких частей и движется без воздействия внешних сил, то какие бы взаимные перемещения частей ни осуществлялись, сумма количеств движения всех частей остается неизменной.
Применительно к ракете, этот закон означает, что прирост количества движения ракеты равен количеству движения уходящих газов, образующихся в результате горения. Модель строится исходя из рассмотрения выхлопа одной ничтожно малой порции газов, имеющей массу dm, вылетающей из сопла со скоростью V0 – она называется скоростью истечения газов относительно ракеты. Составим уравнение, в левой части которого будет стоять увеличение количества движения ракеты массой m (она после выхлопа приобретает увеличение скорости dv), а в правой – количество движения выброшенных газов (знак минус перед dm ставится оттого, что масса m уменьшается).
Решение этого дифференциального уравнения имеет вид:
где m0 – начальная масса ракеты, определяемая из начального условия при старте v=0. Таким образом, скорость ракеты выражается формулой:
Это формула Циолковского. Данная модель объясняет, как нарастает скорость ракеты по мере сжигания топлива. Характер процесса нагляднее всего уяснить с помощью графика (Рис8), показывающего изменение скорости с уменьшением массы ракеты.
Рис.8. Изменение скорости ракеты Приведенная модель достаточно проста, поскольку не учитывает сопротивление воздуха, земное тяготение. Учет их резко усложняет модель и анализ результатов решения. Решение лежит на поверхности, но оно возникло только тогда, когда появилась проблема. Точно так при решении практических задач возникают открытия. А решение может оказаться очень простым. Можно утверждать, что моделирование используется в любой сфере человеческой деятельности и при любом уровне значимости решаемых проблем: от решения конкретных инженерных задач до проведения научных исследований. Моделирование стало применяться еще в глубокой древности и постепенно, с развитием цивилизации, захватывало практически все области жизнедеятельности человека. Люди начали пользоваться, например, математическими моделями еще до осознания математики как самостоятельной науки – достаточно вспомнить исчисление площадей в Древнем Египте. Как только начала развиваться цивилизация, так человек решая практические задачи начал использовать модели объектов (планировка городов, строительство зданий, и т.п.). Человек, просто не осознавая, в своей жизни все время создает и использует всевозможные модели: модели окружающего пространства, модели поведения других людей, модели физических и технических объектов и т.д., с тем, чтобы получить практическую пользу. Например, переходя дорогу, мы моделируем движение приближающейся машины, чтобы предсказать, успеем ли безопасно перейти, и выбрать правильное решение. В настоящее время нельзя назвать область человеческой деятельности, в которой в той или иной степени не использовались бы методы моделирования.
ТЕМА 3
|

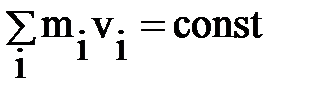
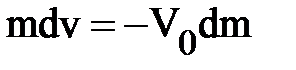 , или
, или 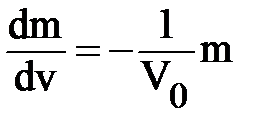 .
.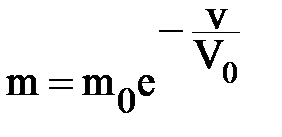 ,
,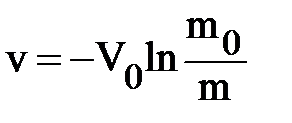 .
.


