Современная стоимость постоянной ренты постнумерандо
Годовая рента. Пусть имеется годовая рента постнумерандо, член которой равен R, срок ренты – n, ежегодное дисконтирование. Рента немедленная. В этих условиях дисконтированная величина первого платежа равна Современная стоимость ренты равна сумме членов этой прогрессии:
Множитель, на который умножается При увеличении срока ренты величина
Полученное выражение используется при расчете современной стоимости вечной ренты. Определим взаимосвязь коэффициентов приведения ограниченной и вечной рент:
В этой формуле искомый коэффициент приведения определен как доля коэффициента приведения вечной ренты, зависящей от срока ренты. Формула
может быть применена и для определения современной стоимости р -срочной ренты. В этом случае переменная Коэффициент приведения ренты за срок
|
; второго - 
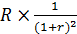; последнего - 
. Эти величины образуют ряд, соответствующий геометрической прогрессии с первым членом 
.
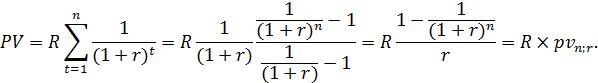
, называется коэффициентом приведения ренты, он обозначен как 
. Этот коэффициент характеризует современную стоимость ренты с членом, равным 1.
предельное значение коэффициента составит
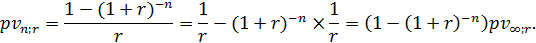
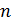означает число периодов ренты, а 
- ставку за один период.
определяется следующим образом:
