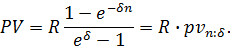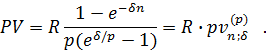Годовая рента с начислением процентов m раз в годуВ формуле
Заменим дисконтный множитель
Рента р-срочная (
Рента р-срочная (p = m). Число членов ренты здесь равно числу начислений процентов; величина члена ренты составляет
Рента р-срочная (p ≠ m). Сумма членов соответствующей прогрессии составит
Ренты с непрерывным начислением процентов. Пусть ряд состоит из ежегодных платежей, равных R, однако проценты начисляются непрерывно, сила роста равна δ. При дисконтировании по этой ставке всех членов ряда получим геометрическую прогрессию с первым членом R и знаменателем
Если имеет место р -срочная рента с непрерывным начислением процентов, то
|
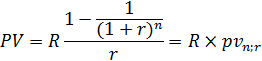
на эквивалентную величину 
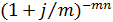и, соответственно, 
заменим на 
, после чего имеем:
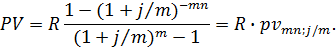
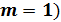. Если платежи производятся не один, а р раз в году, то коэффициенты приведения находятся также, как это было сделано для годовой ренты. Только в этом случае размер платежа равен 
, а число членов составит np. Сумма дисконтированных платежей в этом случае равна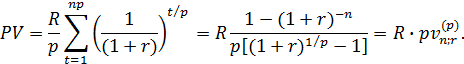
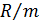. В итоге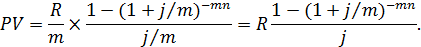
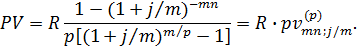
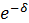. Сумма членов прогрессии находится следующим образом:
