Решение. . . .dQ = Ср × dT
Q = Ср (Т 2 – Т 1) Q (Н2О) = 4.18 (373 – 298) = 313.5 [Дж/г× К] Q (Fe) = 0.448 (373 – 298) = 33.6 [Дж/г× К]. Не случайно в жаркий солнечный день одинаковые по площади и массе водные и металлические поверхности по-разному нагреваются.
Работа Работа А – это форма обмена энергией системы с окружающей средой посредством направленного движения макросистемы как целого. Например, газ в цилиндре под поршнем расширяется и совершает работу, поднимает груз на некоторую высоту. (рис. 35). Работа совершается за счет энергии нагревателя, передаваемой в форме теплоты. Газ совершает направленное движение, перемещая поршень с грузом, поэтому работа является макрофизической формой обмена энергией системы и окружающей среды. Рассмотрим работу расширения (или сжатия), совершаемую идеальным газом. Работа изобарного расширения (р = const) Работа изобарного расширения n моль идеального газа (работа подъема груза на некоторую высоту) осуществляется за счет внешнего источника энергии (нагревателя) в соответствии с уравнением dQр = dU + рdV. Газ, находящийся в цилиндре под поршнем, изменяет внутреннюю энергию (нагревается) и совершает работу. При р = const нагревание газа сопровождается изменением объема от V 1 до V 2. Модель такого процесса представлена на рис. 35. Интегрируем уравнение dA = p dV
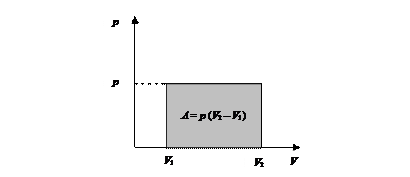
А = р (V 2 – V 1). (4.18) Графически в координатах р – V работа изобарного расширения представлена площадью (рис. 38).
Рис. 38. Работа изобарного расширения
Для n моль исходное и конечное состояния идеального газа выражаются уравнениями. PV 1 = nRT 1 и PV 2 = nRT 2. Заменим объемы в уравнении (4.18), тогда
Из уравнений (4.18) и (4.19) следует, что работа расширения идеального газа при постоянном давлении есть функция состояния. Она определяется только начальным и конечным состояниями системы. В данном случае начальное и конечное состояния определяются значениями V и T. Работа изотермического расширения (Т = const) Работа изотермического расширения n моль идеального газа также осуществляется за счет внешнего источника энергии (нагревателя, или термостата), но при этом изменяется давление в системе так, как это представлено на рис. 39. Внутренняя энергия идеального газа является функцией температуры. При Т = const dU = 0, и уравнение первого закона термодинамики принимает вид:
dQ = рdV
Рис. 39. Расширение газа по мере уменьшения груза (количества песчинок) на поршне: а) исходное состояние; б) конечное состояние системы
Интегрируем уравнение dA = p dV
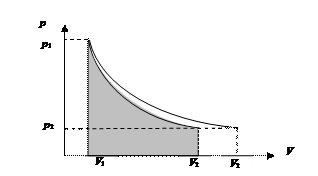
Графически в координатах р – V работа изотермического расширения представлена площадью, показанной на рис. 40.
Рис. 40. Работа изотермического расширения
Работа адиабатического расширения (dQ = 0) В адиабатическом процессе система обменивается с окружающей средой энергией только в форме работы (dQ = 0), поэтому работа адиабатического расширения осуществляется за счет внутренней энергии n моль идеального газа (рис. 41).
Рис. 41. Адиабатическое расширение (сжатие) идеального газа
При dQ = const уравнение первого закона термодинамики принимает вид: 0= dU + dА. Так как работа расширения в адиабатическом процессе происходит за счет уменьшения внутренней энергии системы, то при расширении газ охлаждается, при сжатии – разогревается. Из уравнения (4.13) dU =n CVdT, тогда dА = - nCVdT
А =nСV (Т 1 – Т 2) (4.21) В координатах p – V уравнения изотермы и адиабаты имеют вид рV = const и
Рис. 42. Работа адиабатического расширения (закрашенная область) меньше, чем работа изотермического расширения в одной и той же области изменений давления
Для изохорного процесса (V = const) работа расширения равна А = 0.
|
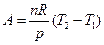. (4.19)
(4.20)
const соответственно, где 
. Графически в координатах р – V работа адиабатического расширения представлена площадью, изображенной на рис. 42.
