Энтропия. Обратимся к модели самопроизвольного необратимого превращения энергии на примере механической модели
Обратимся к модели самопроизвольного необратимого превращения энергии на примере механической модели, предложенной Эткинсом (рис. 44). Потенциальная энергия падающего тела превращается в энергию движения микрочастиц поверхности пола. Энергия системы остается постоянной, происходит лишь ее перераспределение. Обратный процесс перемещения тела из состояния 2 в состояние 1 невозможен. Тело самопроизвольно не вернется в исходное состояние, т.к. частицы, расположенные на поверхности пола, рассеяли полученную энергию по всей поверхности пола в результате межмолекулярных соударений.
Рис. 44. Модель рассеяния энергии (увеличения беспорядка) в результате падения шарика на поверхность пола. Цифрами обозначены: 1 - начальное, 2 - конечное состояние системы. Стрелки указывают направление самопроизвольного (необратимого) процесса. Система изолирована от окружающей среды
Обычно математическое выражение второго закона термодинамики дается на примере цикла Карно или выводится с использованием принципа Каратеодори. Мы ограничимся следующим уравнением второго закона термодинамики
принимая его как закон, который, как и любой фундаментальный закон, не выводится. Для термодинамически равновесного (обратимого) процесса уравнение (4.22) принимает вид: dS обр. В термодинамически неравновесном (необратимом) процессе dSнеобр. Изменение энтропии как критерий направления процесса применим к изолированным системам. Так как изолированная системане обменивается энергией с окружающей средой, для нее dQ = 0 и, соответственно, для состояния термодинамического равновесия в изолированной системе
dS сист. = 0 (4.25) для необратимого процесса, протекающего в изолированной системе dS сист. > 0. (4.26) Одна из формулировок второго закона термодинамики гласит: любой необратимый процесс характеризуется увеличением энтропии изолированной системы (dS сист. > 0) и любой обратимый процесс характеризуется неизменностью энтропии изолированной системы (dS сист. =0). На примере изолированной системы, состоящей из горячего и холодного тел (рис. 45), покажем, что процессы обмена энергией в форме теплоты между телами сопровождаются ростом энтропии. Изменение энтропии системы равно сумме изменений энтропии входящих в состав данной системы тел. dS сист. = dS1 + dS2 или dS сист. Горячее тело при Т 1 обменивает с холодным телом, находящимся при температуре Т 2, бесконечно малое количество энергии. Количество теплоты δ Q настолько малое, что температура тел практически не меняется и Т 1 > > Т 2.
Рис. 45. Обмен энергией горячего (Т1) и холодного (Т2) тел в изолированной системе
В соответствии с принятой в термодинамике шкалой δ Q < 0 для горячего тела и δ Q > 0 для холодного. Следовательно, в уравнении (4.27) отношение
Таким образом, только самопроизвольные процессы передачи тепла от горячего тела к холодному протекают в изолированной системе.
|


 , (4.22)
, (4.22) (4.23)
(4.23) . (4.24)
. (4.24) . (4.27)
. (4.27)
 , а
, а  . По абсолютной величине
. По абсолютной величине 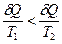 , следовательно
, следовательно > 0.
> 0.


