МЕТОДИЧЕСКИЕ УКАЗАНИЯ. Окружающие нас тела по сути представляют собой пустоту
Размерность всех членов в 3.33 [Дж/кг]
Для жидкой частицы можно записать, что её энергия (Э) равна:
где ПП – потенциальная энергия положения в поле сил тяжести; ПС – потенциальная энергия состояния; К – кинетическая энергия.
Рассматривая приведённые выше зависимости с уравнением (*) перепишем
А удельная механическая энергия, то есть отнесённая к единице массы:
Из уравнения 3.33 и 3.35 энергетический смысл уравнения Бернулли: Удельная механическая энергия идеальной не сжимаемой жидкости остаётся постоянной вдоль элементарной струйки. Таким образом интеграл Бернулли выражает собой закон сохранения механической энергии для элементарной струйки. То есть является энергетическим уравнением. В практических расчётах уравнения 3.31 и 3.32 используют в следующих формах:
Обычно используют это уравнение при исследовании движения газа в вентиляционных сетях и каналах. При постоянной плотности капельной жидкости (вода, масло и т.д.) используют уравнение в виде ….3.37 Это уравнение удобно использовать расчёта водопроводов (гидромагистралей), насосов. Также уравнение 3.31 часто записывают с учётом параметров потока, например в сечении 1-1 и 3-3 на рис.3.4
2.8.3 Уравнение Бернулли для элементарной струйки реальной жидкости. Очевидно, что удельная механическая энергия для вязкой жидкости будет определяться теми же составляющими, что и для невязкой (идеальной) жидкости. Но значение полной удельной энергии в каждом сечении реальной жидкости будет неодинаковым. Так как часть энергии вязкой жидкости расходуется на работу против сил внутреннего трения(на преодоление гидравлических сопротивлений), при этом происходит диссипация(потеря) механической энергии. То есть энергия потока в каждом последующем сечении будет меньше чем в предыдущем на величину потерь энергии между этими сечениями. Из этих соображений при постоянной плотности получим уравнение Бернулли для струйки жидкости:
Аналогично записывая уравнения для струйки сжимаемого вязкого газа. Например при изотермическом процессе:
где p1, p2 – давление среды в сечении 1 и 2; po, ρ 0 – давление и плотность среды в нормальных условиях
2.8.4 Уравнение Бернулли для потока конечных размеров Понятно, что поток конечных размеров можно рассматривать состоящим из большого числа элементарных струек. Следовательно, энергию переносимую потоком через произвольное сечение, можно посчитать суммированием энергии элементарных струек.
где
Интегрирование уравнения 3.42 в общем случае не возможно. Вводят ограничение: элементарные струйки движутся параллельно или искривлены очень слабо. Экспериментально и теоретически установлено, что для этих условий в пределах живого сечения выполняется следующее:
С учётом этого условия 3.42 для несжимаемой жидкости представляют в следующем в
|


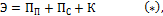
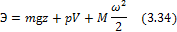
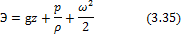

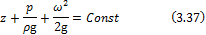



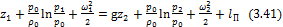 ,
,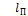 – потерянная удельная энергия между сечениями элементарной струйки;
– потерянная удельная энергия между сечениями элементарной струйки;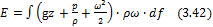 ,
,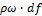 - элементарный массовый расход.
- элементарный массовый расход.



