Постановка экспериментальной задачи
В данной работе осуществляется экспериментальная проверка основного уравнения динамики вращательного движения (4.8) с помощью маятника Обербека. Маятник представляет собой маховик, которому придана крестообразная форма (рис. 4.1). По четырем взаимно-перпендикулярным стержням могут перемещаться грузы массой m 0. На общей оси находится шкив, на который наматывается нить с привязанным к ней грузом массой m. Под действием падающего груза нить разматывается и приводит маховик в равноускоренное вращательное движение. При этом угловое ускорение крестовины определяется соотношением:
В свою очередь, пользуясь известным выражением для равноускоренного движения груза:
(h – высота падения груза, t – время падения груза) находим:
или, используя (4.9):
Момент силы, приложенной к маятнику, находим по формуле (4.7), где: F – сила, действующая на шкив. Но Силу F можно найти из уравнения движения груза:
где: m – масса падающего груза, а
Используя формулу (4.8) получим:
Определив экспериментально значения h и t, при заданных параметрах r и m, по формуле (4.15) находим значение момента инерции маятника Обербека. Теоретическое значение момента инерции маятника можно рассчитать следующим образом:
где: m 0 = 0, 114 кг – масса подвижного груза крестовины; R – расстояние от центра масс подвижного груза до оси вращения; r 0= 0, 015 м – радиус груза; l = 0, 02 м – длина образующей груза. Момент инерции системы без грузов J 0 можно определить по формуле:
где: l 1 = 0, 15 м – длина одного из стержней крестовины; m 1= 0, 023 кг – масса стержня.
|

 , (4.9)
, (4.9) где: а – ускорение падающего груза, r = d/ 2 – радиус шкива.
где: а – ускорение падающего груза, r = d/ 2 – радиус шкива. , (4.10)
, (4.10) , (4.11)
, (4.11) . (4.12)
. (4.12) , и
, и 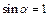 . Тогда формула (4.7) имеет вид:
. Тогда формула (4.7) имеет вид:  .
. , (4.13)
, (4.13) ,
,  – сила натяжения нити. Тогда для момента силы получим следующее выражение:
– сила натяжения нити. Тогда для момента силы получим следующее выражение: . (4.14)
. (4.14) . (4.15)
. (4.15)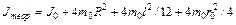 , (4.16)
, (4.16) , (4.17)
, (4.17)


