Методы исследования и виды движения жидкости

 

Кинематика жидкости и газа имеет существенные отличия от кинематики твердого тела. Частицы твердого тела жестко связаны между собой. В движущейся жидкости (газе) такие связи отсутствуют, частицы движутся не только вместе с потоком, но и относительно друг друга.

Существует два аналитических способа исследования движения жидкости: метод Лагранжа и метод Эйлера.

Метод Лагранжа позволяет исследовать кинематику движения частицы жидкости в пространстве относительно начальных координат x₀, y_0, z₀ в момент времени t₀. Текущие координаты x, y_, z движущейся частицы определяются относительно начальных координат. Зная текущие координаты в различные моменты времени можно построить траекторию движения частицы, а поток жидкости представить совокупностью траекторий частиц за определенный промежуток времени. Этот метод из-за сложности в механике жидкости и газа применяется достаточно редко.

Метод Эйлера изучает определенную область пространства, в которой находится движущаяся жидкость. В этой области выбираются неподвижные точки, в которых определяются скорость и давление в определенные моменты времени. Этот метод позволяет определить поля скоростей и давлений в определенный момент времени и используется чаще всего в настоящее время.

Движение жидкости может быть установившимся (стационарным) и неустановившимся (нестационарным).

Установившимся называется движение жидкости, при котором скорость и давление в любой неподвижной точке пространства, занятого жидкостью, не изменяются во времени, т.е.

 

p=f₁(x, y, z); u=f₂(x, y, z).

 

В частном случае установившееся движение может быть равномерным, когда поле скоростей не меняется вдоль потока жидкости (газа). Примером установившегося движения является движения теплоносителя в системе отопления при неизменных регулировках, движение жидкости в напорном трубопроводе центробежного насоса при постоянной частоте вращения, в реках при отсутствии паводков и проливных дождей.

Частным случаем установившегося движения является равномерное течение жидкости – когда поперечное сечение и средняя скорость не меняются по длине потока.

Неустановившимся называется движение жидкости, когда давление и (или) скорость изменяются во времени в любой неподвижной точке рассматриваемого пространства с движущейся жидкостью. При этом имеют место следующие зависимости:

 

p=f₃(x, y, z, t); u=f₄(x, y, z, t).

В качестве примеров неустановившегося движения можно привести: движение жидкости во всасывающем трубопроводе поршневого насоса, движение воды в реке во время половодья.

В дальнейшем рассмотрим установившееся движение жидкости и некоторые частные случаи неустановившегося движения.

Кроме того, различают напорное и безнапорное движение жидкости.

Напорное движение – движение жидкости, происходящее за счет перепада напоров (чаще всего из-за перепада давления) при отсутствии свободной поверхности. Примером напорного течения является движение воды в водопроводной сети жилого дома, масла в гидроприводе строительной машины. Когда поток имеет свободную поверхность, то такое движение жидкости называется безнапорным. Оно происходит за счет перепада высот. Безнапорным является движение воды в реках, каналах.

Основные понятия струйчатой модели потока жидкости

При установившемся движении жидкости траектории частиц не изменяются во времени. Траектории различных частиц жидкости, проходящих через данную точку пространства при неустановившемся движении, различны. Поэтому для изучения характеристик потока в данный момент времени введено понятие линии тока.

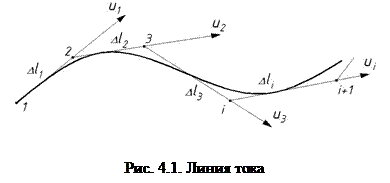Линия тока – кривая, в каждой точке которой вектор скорости частицы жидкости направлен по касательной к ней. Пусть в данный момент времени t₁ через неподвижную точку 1 пройдет частица жидкости, вектор скорости в этой точке u₁. Отложим на этом векторе элементарное расстояние Δ l₁ и получим точку 2 (рис. 4.1) и т.д. Если расстояния между точками Δ l будут стремиться к нулю, то получим кривую, которая и будет линией тока. При неустановившемся движении в следующий момент времени вектор скорости в точке 1 может быть другим. Поэтому линия тока в случае неустановившегося движения характеризует картину движения только в данный момент времени. При установившемся движении линия тока совпадает с траекторией частицы и не меняется с течением времени.

Если в движущейся жидкости взять замкнутый контур, ограничивающий поверхность бесконечно малых площадок dS, и через все его точки провести линии тока, то получим трубчатую поверхность, называемую трубкой тока (рис. 4.2).

Часть потока жидкости, заключенного внутри трубки тока, называется элементарной струйкой.

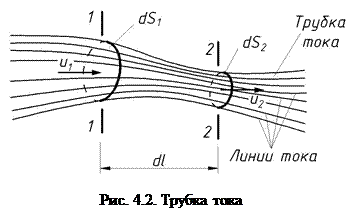Скорости частиц жидкости направлены по касательной к поверхности трубки тока, а нормальные составляющие скорости отсутствуют. Поэтому при установившемся движении ни одна частица жидкости не может проникнуть сквозь поверхность трубки тока. Следовательно, трубка тока является непроницаемой, а поток жидкости можно представить состоящим из бесчисленного множества элементарных струек. Скорости движения жидкости и давление в различных точках поперечного сечения элементарной струйки dS постоянны и одинаковы. Форма струйки, площади dS и скорости изменяются по длине струйки. В потоке жидкости из-за различия скоростей в струйках происходит относительное скольжение струек относительно друг друга. Для неустановившегося течения эти положения справедливы только в данный момент времени.