Дифференциальные уравнения Эйлера движения идеальной жидкости
где m – масса параллелепипеда: m = ρ dx dy dz; аХ – проекция ускорения параллелепипеда на ось Х: аx = dux/dt. Проведя рассуждения, аналогичные подразделу 3.3, получим:
Равнодействующая массовой силы dG равна:
dGx=ρ dx dy dz j,
где j – ускорение, вызванное силой dG. Тогда проекция dG на ось Х будет иметь вид: dGх=ρ dx dy dz jх. Подставим соответствующие значения проекций сил в уравнение (5.1) и разделим на ρ dx dy dz. В результате получим:
Проведя аналогичные рассуждения для осей Y и Z, получим дифференциальные уравнения движения жидкости:
Система уравнений (5.2) называется системой дифференциальных уравнений Эйлера движения идеальной жидкости. Эти уравнения справедливы как для несжимаемой, так и для сжимаемой жидкости. При выводе уравнений (5.2) не накладывались условия стационарности движения, значит они справедливы и для неустановившегося движения. Для удобства практического использования вместо системы уравнений (5.2) получим одно эквивалентное уравнение. Для этого умножим первое уравнение системы (5.2) на dx=ux dt, втрое – на dy=uy dt, третье – на dz=uz dt и сложим эти уравнения. В результате получим:
Трехчлен, находящийся в скобках, является полным дифференциалом давления dp (см. 3.3). Кроме того, ux dx= d(u2x/2), uy dy= d(u2y/2), uz dz= d(u2z/2), а d(u2x/2)+ d(u2y/2)+ d(u2z/2)= d(u2/2). С учетом этого уравнение (5.3) примет вид:
Уравнение (5.4) называют дифференциальным уравнением Эйлера движения идеальной жидкости.
|

 В потоке идеальной жидкости расположим декартовы оси координат произвольным образом. Так же, как и при рассмотрении равновесия покоящейся жидкости (см. п. 3.3), выделим в первом квадранте элементарный объем в виде параллелепипеда с ребрами dx, dy и dz, параллельными соответствующим осям координат (рис. 5.1). Предположим, что жидкость в нем затвердела. Тогда на грани параллелепипеда действуют силы давления dF1…6 от окружающей жидкости, а в его центре масс (точка О) приложена сила тяжести dG. Параллелепипед движется со скоростью u. Составим уравнение движения данного параллелепипеда, используя принцип Д ' Аламбера. Уравнение движения параллелепипеда, спроектированное на ось Х, имеет вид:
В потоке идеальной жидкости расположим декартовы оси координат произвольным образом. Так же, как и при рассмотрении равновесия покоящейся жидкости (см. п. 3.3), выделим в первом квадранте элементарный объем в виде параллелепипеда с ребрами dx, dy и dz, параллельными соответствующим осям координат (рис. 5.1). Предположим, что жидкость в нем затвердела. Тогда на грани параллелепипеда действуют силы давления dF1…6 от окружающей жидкости, а в его центре масс (точка О) приложена сила тяжести dG. Параллелепипед движется со скоростью u. Составим уравнение движения данного параллелепипеда, используя принцип Д ' Аламбера. Уравнение движения параллелепипеда, спроектированное на ось Х, имеет вид: , (5.1)
, (5.1)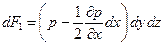 , а
, а  .
.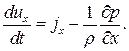

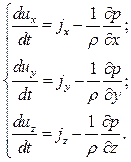 (5.2)
(5.2)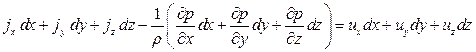 . (5.3)
. (5.3) (5.4)
(5.4)


