Гидравлические потери напора
В соответствии с многочисленными экспериментальными исследованиями потери пьезометрического напора (удельной потенциальной энергии давления) в общем случае зависят от формы, размеров, шероховатости внутренней поверхности стенок трубопровода (канала), скорости и вязкости жидкости, но практически не зависят от давления. Для расчета потерь напора используется формула Вейсбаха:
где ζ – коэффициент сопротивления; Δ рп – потери давления. Потери пьезометрического напора (в дальнейшем просто потери) подразделяются на два вида: потери в местных гидравлических сопротивлениях и потери в линейных гидравлических сопротивлениях. Местные гидравлические сопротивления – короткие участки трубопроводов (каналов), в которых происходит изменение скорости по величине и (или) направлению и, как правило, возникают вихревые зоны. К местным сопротивлениям относятся входы в трубопровод и выходы из него, плавные и внезапные расширения и сужения трубопроводов, повороты, разветвления, вентили и задвижки, клапаны и т.д. Рассмотрим некоторые местные сопротивления.
Для определения потерь напора при внезапном расширении трубопровода запишем уравнение Бернулли для сечений 1-1 и 2-2 при следующих допущениях: - касательные напряжения на стенке трубы между сечениями 1-1 и 2-2 на стенке трубы равны нулю, т.е. пренебрегаем силами трения, считая их значительно меньше сил давления; - давление р1 в сечении 1-1 равномерно действует по всей площади S2 в месте внезапного расширения трубопровода, т. к. поток жидкости еще сохранил свой поперечный размер и, соответственно, скорость и давление еще не изменились; - во всех точках сечений 1-1 и 2-2 скорости практически равны соответствующим средним скоростям u1 и u2, при этом α 1= α 2=1. С учетом этих допущений уравнение Бернулли примет вид:
hвр – потери напора при внезапном расширении трубопровода. Воспользуемся теоремой Эйлера об изменении количества движения:
где
Разделим правую и левую части данного уравнения на ρ gS2. С учетом того, что u2=Q/S2 получим:
Преобразуем данное уравнение
или
Сравним уравнения (5.17) и (5.18). Очевидно, что потери напора при внезапном расширении трубопровода будут равны:
Уравнение (5.19) называют теоремой Борда – Карно в честь французских ученых Ж. Борда (получил уравнение аналитически) и Н. Карно (экспериментально его подтвердил). Экспериментально установлено, что уравнение (5.19) справедливо при Re > 3500, поскольку сделанные выше допущения не применимы для ламинарного течения. Преобразуем уравнение (5.19) с учетом условия u2=u1S1/ S2:
Тогда коэффициент сопротивления при внезапном расширении трубопровода ζ вр будет равен:
Когда S2→ ∞, например при выходе потока жидкости в неограниченный объем, ζ вр = ζ вых=1. Внезапное сужение трубопровода (рис. 5.6). Потери напора складываются из двух составляющих: потери напора на сжатие потока, так как частицы обтекают входной угол по определенной кривой, в результате его сечение становиться меньшим, чем S2; потери напора при последующем расширении потока до сечения S2 (определяются с помощью теоремы Борда-Карно). Тогда потери напора при внезапном суженении потока hвс будут равны:
где ζ с – коэффициент сопротивления, обусловленный сужением потока до Sс; uс – средняя скорость потока в суженном месте.
В частном случае, когда S1→ ∞, например, при выходе трубы из резервуара достаточно больших размеров, можно считать S1/S2=0. Тогда коэффициент сопротивления ζ вс=0, 5. С помощью закругления входной кромки можно существенно уменьшить коэффициент сопротивления и, соответственно, потери напора. Поворот трубопровода. Внезапный поворот трубопровода (колено) вызывает значительные потери напора, так как в нем происходит отрыв потока от стенок и вихреобразование (рис. 5.7). Потери напора зависят от угла поворота δ, с увеличением δ потери возрастают, при δ =900 коэффициент сопротивления равен ζ вп=1, 1. Для уменьшения потерь напора поворот выполняют плавным.
Диаметр трубопровода d и плотность ρ при этом вводятся в компьютер вручную. В случае, когда труба некруглая, то зависимость для расчета ζ м имеет вид:
При этом вручную вводятся площадь сечения трубопровода S и плотность ρ;. В некоторых случаях площади сечений трубопровода на входе и выходе местного сопротивления различны. При этом уравнение Бернулли для сечений на входе и выходе данного сопротивления будет следующим (считаем течение турбулентным, т.е. α вх= α вых≈ 1):
Преобразуем уравнение (5.26):
Решим уравнение (5.27) относительно ζ м:
С учетом, что uвх=Q/Sвх и uвых=Q/Sвых получим:
где Sвх и Sвых – площади живых сечений трубопровода на входе и выходе местного сопротивления, соответственно. Для большинства местных сопротивлений коэффициенты ζ м определены ранее и приведены в справочниках. Поэтому, при выполнении инженерных расчетов для определения потерь напора в местных сопротивлениях hм используется формула Вейсбаха, а коэффициент сопротивления ζ м выбирается по справочнику:
Линейные гидравлические сопротивления – прямолинейные участки трубопроводов (каналов) постоянного сечения. для линейных сопротивлений коэффициент ζ л пропорционален относительной длине трубопровода l/d и равен:
где l – длина прямолинейного участка трубопровода постоянного сечения диаметром d; λ – коэффициент гидравлического трения или коэффициент Дарси. Тогда формула Вейсбаха (5.16) примет вид:
Формула (5.31) называется формулой Дарси – Вейсбаха. Когда труба некруглая или круглая труба не полностью заполнена жидкостью, то вместо диаметра трубы d подставляется гидравлический диаметр Dг, т.е.
Многочисленные исследования потерь напора в линейных гидравлических сопротивлениях позволили выделить пять основных областей сопротивления. I область. Область ламинарного течения: Re< 2300. В этой области λ зависит только от числа Рейнольдса и определяется следующей зависимостью:
Эта зависимость вытекает из закона Пуазейля – Гагена
II область. Область перехода от ламинарного течения к турбулентному: Re=2300…4000. В этой области λ также зависит только от числа Рейнольдса и определяется по формуле Н. Френкеля:
III область. Область гидравлически гладких труб, режим течения турбулентный: Re=4000…20 d/Δ э (Δ э – абсолютная величина, эквивалентная по сопротивлению равномерно-зернистой шероховатости в опытах И. Никурадзе*). В этой области λ зависит только от числа Рейнольдса и не зависит от шероховатости стенок трубы. Причиной этого является тонкий ламинарный слой, который присутствует при турбулентном течении жидкости у стенок трубы (рис. 5.9). Толщина этого слоя δ л определяется по эмпирической формуле:
При 4000< Re< 3·106 целесообразно использовать формулу Конакова:
IV область. Область доквадратичного сопротивления, режим течения турбулентный: Re=20 d/Δ э…500 d/Δ э, а δ л≈ Δ э (рис. 5.11) В этой области λ зависит от числа Рейнольдса и относительной шероховатости стенок трубы Δ э /d. Для определения λ в этой области наиболее часто используют формулу А.Д. Альтшуля:
V область. Область квадратичного сопротивления (шероховатых труб), режим течения турбулентный: Re> 500 d/Δ э, а δ л< Δ э. В этой области λ зависит только от относительной шероховатости стенок трубы Δ э /d. Для определения λ в этой области наиболее часто используют формулу Прандтля – Никурадзе: ___ * Иван Ильич Никурадзе родился в 1894 г. в гор. Самтредия (Грузия), закончил гимназию в городе Кутаиси и поступил (вместе с братом) в Тбилисский университет. В 1919 г. он был зачислен в группу студентов, направленных для обучения в зарубежные страны. И.Никурадзе учился в Гетингенском университете и в 1923 г. успешно защитил докторскую диссертацию под руководством Л.Прандтля " Наблюдения на распределение скорости в турбулентном течении". Провел экспериментальные исследования гидравлического сопротивления труб с искусственной равномерно-зернистой шероховатостью. Шероховатость была получена путем приклейки песчинок определенного поперечного размера Δ на внутреннюю поверхность трубы.
При проведении инженерных гидравлических расчетов и определении λ по изложенной выше методике целесообразно использовать программный пакет Mathcad. Во Всесоюзном теплотехническом институте (СССР) в первой половине ХХ века под руководством Г.А. Мурина проведены экспериментальные исследования труб с естественной шероховатостью по определению их гидравлического сопротивления. По результатам исследований в полулогарифмических координатах построены графики зависимостей λ =f(Re, d/ Δ э) (рис. 5.12). Этими графиками можно пользоваться при выполнении разовых расчетов, не требующих высокой точности. При расчете потерь напора во всем трубопроводе допускается, что каждое сопротивление независимо от соседних. Поэтому общие потери рассчитываются как сумма потерь в каждом сопротивлении (принцип наложения):
|

 (5.16)
(5.16) Внезапное расширение трубопровода (рис. 5.5). Поток, выходящий из трубы меньшего сечения S1, не сразу заполняет поперечное сечение трубы большего сечения S2. Жидкость в месте расширения отрывается от стенок и дальше движется в виде струи, отделенной от остальной жидкости поверхностью раздела ас. Между струей и поверхностью трубопровода образуется кольцевая область вихревого движения жидкости авс. В этой области жидкость не участвует в общем поступательном движении, хотя обмен частицами жидкости между областью вихревого движения и струей постоянно происходит. Для обеспечения вихревого движения в области авс необходима энергия, чем и обусловлены потери напора. Струя постепенно расширяется и на некотором расстоянии от места увеличения диаметра заполняет все сечение трубы большего диаметра.
Внезапное расширение трубопровода (рис. 5.5). Поток, выходящий из трубы меньшего сечения S1, не сразу заполняет поперечное сечение трубы большего сечения S2. Жидкость в месте расширения отрывается от стенок и дальше движется в виде струи, отделенной от остальной жидкости поверхностью раздела ас. Между струей и поверхностью трубопровода образуется кольцевая область вихревого движения жидкости авс. В этой области жидкость не участвует в общем поступательном движении, хотя обмен частицами жидкости между областью вихревого движения и струей постоянно происходит. Для обеспечения вихревого движения в области авс необходима энергия, чем и обусловлены потери напора. Струя постепенно расширяется и на некотором расстоянии от места увеличения диаметра заполняет все сечение трубы большего диаметра. (5.17)
(5.17)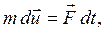
 – изменение количества движения, обусловленное импульсом внешних сил
– изменение количества движения, обусловленное импульсом внешних сил  . Применим эту теорему к объему жидкости, заключенному между сечениями 1-1 и 2-2. Тогда равнодействующая внешних сил, действующих на рассматриваемый объем, будет равна (р1- р2)S. Изменение количества движения в этом случае можно определить следующим образом: Q ρ dt(u2 - u1). Подставим данные значения в теорему Эйлера. Тогда
. Применим эту теорему к объему жидкости, заключенному между сечениями 1-1 и 2-2. Тогда равнодействующая внешних сил, действующих на рассматриваемый объем, будет равна (р1- р2)S. Изменение количества движения в этом случае можно определить следующим образом: Q ρ dt(u2 - u1). Подставим данные значения в теорему Эйлера. Тогда


 (5.18)
(5.18) (5.19)
(5.19) (5.20)
(5.20) (5.21)
(5.21) (5.22)
(5.22) При выполнении инженерных расчетов для определения ζ с можно пользоваться полуэмпирической формулой И.Е. Идельчика:
При выполнении инженерных расчетов для определения ζ с можно пользоваться полуэмпирической формулой И.Е. Идельчика: (5.23)
(5.23) Как правило, для местных сопротивлений, коэффициент сопротивления ζ м определяется экспериментально. Схема автоматизированного стенда для определения коэффициентов местных сопротивлений приведена на рис. 5.8. Местное сопротивление 1 располагается горизонтально и через него пропускается поток жидкости. с помощью точных датчиков 2 и 3 определяется давление до сопротивления рвх и после рвых, а также расход жидкости Q с помощью расходомера 4. Информация о давлении и расходе в виде электрических сигналов поступает в устройство сбора данных 5, а затем в компьютер 6, где с помощью специальной программы производится обработка данных, поступающих с устройства 5. В случае, когда диаметры трубопровода до и после местного сопротивления равны, расчет коэффициента местного сопротивления ζ м выполняется с помощью зависимости, полученной из уравнений (4.6) и (5.16):
Как правило, для местных сопротивлений, коэффициент сопротивления ζ м определяется экспериментально. Схема автоматизированного стенда для определения коэффициентов местных сопротивлений приведена на рис. 5.8. Местное сопротивление 1 располагается горизонтально и через него пропускается поток жидкости. с помощью точных датчиков 2 и 3 определяется давление до сопротивления рвх и после рвых, а также расход жидкости Q с помощью расходомера 4. Информация о давлении и расходе в виде электрических сигналов поступает в устройство сбора данных 5, а затем в компьютер 6, где с помощью специальной программы производится обработка данных, поступающих с устройства 5. В случае, когда диаметры трубопровода до и после местного сопротивления равны, расчет коэффициента местного сопротивления ζ м выполняется с помощью зависимости, полученной из уравнений (4.6) и (5.16):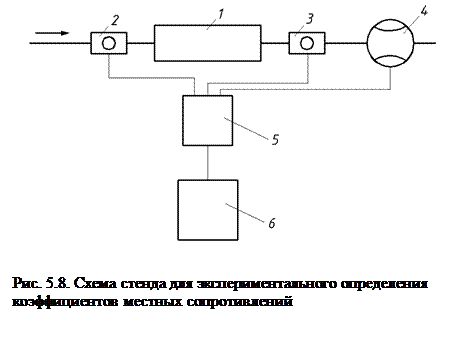
 (5.24)
(5.24) (5.25)
(5.25) (5.26)
(5.26) (5.27)
(5.27)
 (5.28)
(5.28)
 (5.29)
(5.29)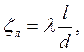 (5.30)
(5.30) (5.31)
(5.31) (5.32)
(5.32) (5.33)
(5.33) (5.34)
(5.34)
 (5.35)
(5.35) (5.36)
(5.36) В этой области δ л> Δ э (рис. 5.10). Для определения λ в этой области при Re< 105 можно пользоваться формулой Блазиуса:
В этой области δ л> Δ э (рис. 5.10). Для определения λ в этой области при Re< 105 можно пользоваться формулой Блазиуса: (5.37)
(5.37) (5.38)
(5.38)
 . (5.39)
. (5.39) (5.40) а также формулу Шифринсона:
(5.40) а также формулу Шифринсона:
 (5.42)
(5.42)


