Расход, средняя скорость. Уравнение расхода (неразрывности)
Расход – количество жидкости, проходящее через живое сечение потока (элементарной струйки) в единицу времени. Данное количество жидкости можно измерять в единицах объема, массы и веса. Поэтому различают объемный Q, массовый Qm и весовой QG расходы. Для элементарной струйки, имеющей бесконечно малые площади живых сечений dS можно считать скорость u одинаковой во всех точек каждого сечения (см. рис. 4.2). Тогда для элементарной струйки объемный dQ, массовый dQm и весовой расходы dQG с учетом уравнений (2.1) и (2.2) будут равны:
Объемный расход потока жидкости можно определить как сумму расходов элементарных струек:
В инженерных расчетах воспользоваться уравнением (4.3) достаточно сложно, поэтому введено понятие средней скорости. Средняя скорость потока – фиктивная скорость, с которой якобы движутся все частицы жидкости в данном живом сечении потока, но расход при этом равен расходу, вычисленному по действительным скоростям элементарных струек. Тогда
Исходя из закона сохранения вещества, сплошности (неразрывности) течения и непроницаемости трубки тока можно утверждать, что при установившемся течении несжимаемой жидкости во всех живых сечениях элементарной струйки расход постоянен (см. рис. 4.2):
Уравнение (4.5) называется уравнением объемного расхода (сплошности, неразрывности) для элементарной струйки. Для потока несжимаемой жидкости с учетом (4.4) получим:
Уравнение (4.6) является частным случаем закона сохранения вещества при условии сплошности (неразрывности) течения. При установившемся движении сжимаемой жидкости (газа) плотность в различных сечениях потока может быть различной, но масса газа, проходящая через живое сечение, будет постоянной. Тогда уравнение расхода для сжимаемой жидкости (газа) будет иметь вид:
Следует отметить, что уравнение (4.7) справедливо и для несжимаемой жидкости. При этом ρ 1= ρ 2= ρ n=const.
|



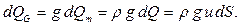
 (4.3)
(4.3) (4.4)
(4.4) (4.5)
(4.5) (4.6)
(4.6) (4.7)
(4.7)


