Лекция 7. Плоский изгиб
Основные понятия и определения. В отличие от деформации растяжения-сжатия и кручения изгиб представляет такую деформацию, при которой происходит искривление оси прямого бруса. Осью бруса называется геометрическое место точек центров тяжестей поперечных сечений бруса. Если в сечении бруса действует только один изгибающий момент, то изгиб называется чистым. Если в поперечных сечениях кроме изгибающего момента действует и поперечная сила, то изгиб называется поперечным. Брус, работающий на изгиб, называется балкой. Изгиб называется плоским, если ось балки после деформации остается плоской линией. В противном случае имеет место косой изгиб. В настоящем разделе рассматривается плоский прямой изгиб. Нормальные напряжения при чистом прямом изгибе. Так как нормальные напряжения зависят только от изгибающих моментов, то вывод формулы для вычисления Статическая задача о плоском изгибе. Изгибающий момент в сечении представляет собой сумму моментов всех элементарных внутренних нормальных сил
Рис. 22 Данное выражение представляет собой статическую сторону задачи о плоском изгибе. Однако его нельзя использовать для определения нормальных напряжений, так как неизвестен закон распределения напряжений по сечению. Геометрическая сторона задачи о плоском изгибе. Выделим двумя поперечными сечениями элемент балки длиной
Рис. 23 Определим длину отрезка волокон, отстоящего от нейтрального слоя на расстоянии
Относительное удлинение в этом случае будет
Зависимость Физическая сторона задачи о плоском изгибе. Используя закон Гука при осевом растяжении, получаем
Подставив в выражение, отражающее статическую сторону задачи о плоском изгибе, значение
откуда
Подставив значение
Данное выражение отражает физическую сторону задачи о плоском изгибе, которое дает возможность рассчитать нормальные напряжения по высоте сечения. Хотя это выражение получено для случая чистого изгиба, но как показывают теоретические и экспериментальные исследования, оно может быть использовано и для плоского поперечного изгиба. Нейтральная линия. Положение нейтральной линии определим из условия равенства нулю нормальной силы в сечениях балки при чистом изгибе
Так как Касательные напряжения. Касательные напряжения, которые возникают в сечениях балки при плоском поперечном изгибе, определяются по зависимости:
где
Касательные напряжения равны нулю в крайних волокнах сечения и максимальны в волокнах нейтрального слоя.
Лекция 8. Плоский изгиб (продолжение) Расчет балок на прочность при изгибе. Прочность балки будет обеспечена, если будут выполняться условия:
Максимальные нормальные напряжения при изгибе возникают в сечениях, где действует максимальный изгибающий момент, в точках сечения наиболее удаленных от нейтральной оси
Максимальные касательные напряжения возникают в сечениях балки, где действует максимальная поперечная сила
Касательные напряжения Построение эпюр поперечных сил и изгибающих моментов. При расчете балок на прочность необходимо знать характер изменения изгибающего момента и поперечной силы вдоль оси балки и знать положение опасного сечения. С этой целью строят эпюры поперечных сил и изгибающих моментов. Поперечная сила Изгибающий момент Если внешняя сила стремится повернуть отсеченную часть по часовой стрелке относительно рассматриваемого сечения, то поперечная сила положительна (рис. 24). Изгибающий момент будет положительным, если при действии момента внешних сил балка искривляется выпуклостью вниз (рис. 25).
Рис. 24
Рис. 25
Построение эпюр поперечных сил и изгибающих моментов рассмотрим на конкретном примере. Пусть на балку действует внешний изгибающий момент
откуда
Рис. 26
Проведем сечения на каждом характерном участке и определим значения поперечной силы В сечении 1
При при
В сечении 2
При при В сечении 3
При при По полученным значениям строим эпюры поперечных сил и изгибающих моментов (рис. 26).
|

 можно производить применительно к чистому изгибу.
можно производить применительно к чистому изгибу.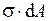 , возникающих на элементарных площадках поперечного сечения балки (рис. 22), относительно нейтральной оси
, возникающих на элементарных площадках поперечного сечения балки (рис. 22), относительно нейтральной оси .
.
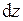 (рис. 23). Под нагрузкой нейтральная ось искривляется (радиус кривизны
(рис. 23). Под нагрузкой нейтральная ось искривляется (радиус кривизны  ), а сечения поворачиваются относительно своих нейтральных линий на угол
), а сечения поворачиваются относительно своих нейтральных линий на угол  . Длина отрезка волокон нейтрального слоя при этом остается неизменной
. Длина отрезка волокон нейтрального слоя при этом остается неизменной .
.

 .
. .
. отражает геометрическую сторону задачи о плоском изгибе, из которой видно, что деформации продольных волокон изменяются по высоте сечения по линейному закону.
отражает геометрическую сторону задачи о плоском изгибе, из которой видно, что деформации продольных волокон изменяются по высоте сечения по линейному закону. .
.


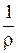 в исходную формулу, получаем
в исходную формулу, получаем
 .
. , то необходимо, чтобы нулю был равен интеграл
, то необходимо, чтобы нулю был равен интеграл 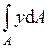 . Данный интеграл представляет собой статический момент сечения относительно нейтральной оси. Так как статический момент сечения равен нулю только относительно центральной оси, следовательно, нейтральная линия при плоском изгибе совпадает с главной центральной осью инерции сечения.
. Данный интеграл представляет собой статический момент сечения относительно нейтральной оси. Так как статический момент сечения равен нулю только относительно центральной оси, следовательно, нейтральная линия при плоском изгибе совпадает с главной центральной осью инерции сечения.
 поперечная сила в рассматриваемом сечении балки;
поперечная сила в рассматриваемом сечении балки; статический момент площади отсеченной части сечения относительно нейтральной оси балки;
статический момент площади отсеченной части сечения относительно нейтральной оси балки; ширина сечения в рассматриваемом слое;
ширина сечения в рассматриваемом слое;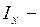 момент инерции сечения относительно нейтральной оси.
момент инерции сечения относительно нейтральной оси. ;
; 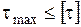 .
.

 обычно малы по сравнению с
обычно малы по сравнению с 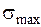 и в расчетах, как правило, не учитываются. Проверка по касательным напряжениям производится только для коротких балок.
и в расчетах, как правило, не учитываются. Проверка по касательным напряжениям производится только для коротких балок. в сечении численно равна алгебраической сумме всех внешних сил справа или слева от сечения.
в сечении численно равна алгебраической сумме всех внешних сил справа или слева от сечения.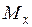 в сечении численно равен алгебраической сумме моментов внешних сил справа или слева от сечения.
в сечении численно равен алгебраической сумме моментов внешних сил справа или слева от сечения.

 и внешняя сила
и внешняя сила 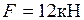 ,
,  . Определим реакции в опорах
. Определим реакции в опорах  . Составим уравнения равновесия моментов всех внешних сил относительно опор
. Составим уравнения равновесия моментов всех внешних сил относительно опор 

 ;
; 


 и изгибающего момента
и изгибающего момента 
 ;
;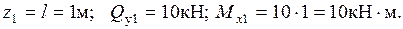

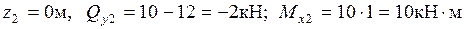 ;
;






