Чистый сдвиг
Напряжения при чистом сдвиге. Чистым сдвигом называют такой вид нагружения, при котором в его поперечных сечениях действует только поперечная сила. Сдвиг, как вид нагружения, встречается редко и имеет место в заклепочных и сварных соединениях.
Рис. 17 При чистом сдвиге (рис. 17) в окрестности точки можно выделить элементарный параллелепипед с боковыми гранями, находящимися под действием одних лишь касательных напряжений. Внутренняя поперечная сила при чистом сдвиге определяется методом сечений. Распределение касательных напряжений принимается равномерным и тогда связь между поперечной силой и касательным напряжением имеет вид:
При чистом сдвиге возникает плоское напряженное состояние, тогда напряжения, действующие на площадке составляющей угол
Касательные напряжения, показанные на рис. 17, по абсолютной величине больше касательных напряжений по любым другим площадкам. Следовательно, они являются экстремальными, а площадки, по которым они действуют – площадками сдвига. Так как по этим площадкам не действуют нормальные напряжения, то их называют площадками чистого сдвига и образуют с главными площадками углы, равные 450. Подставляя угол Следовательно, при чистом сдвиге главные напряжения и экстремальные касательные напряжения равны друг другу. Подставив в уравнения значения углов
При чистом сдвиге нормальные напряжения на любых двух взаимно перпендикулярных площадках равны друг другу по модулю и противоположны по направлению. Деформации при чистом сдвиге. При чистом сдвиге длины ребер элементарного параллелепипеда не изменяются, а изменяются лишь углы между боковыми гранями. Первоначально прямые углы становятся равными Величина
т.е. относительный сдвиг равен углу сдвига.
Рис. 18 Угол сдвига
где Объемная деформация и потенциальная энергия при сдвиге. Относительное изменение объёма при сдвиге определяется из объёмного закона Гука
Величина Полная удельная потенциальная энергия
Учитывая, что при чистом сдвиге
Работа при чистом сдвиге. В результате деформации выделенного параллелепипеда работа силы будет определяться по выражению
где
Ее величина будет равна
где Учитывая, что
Так как работа силы при статическом действии числена равна потенциальной энергии, имеем
Удельная потенциальная энергия в этом случае равна
Приравнивая полученные выражения для удельной потенциальной энергии, получаем соотношение
откуда получаем связь между модулем упругости первого рода
|



 откуда
откуда 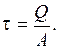
 с вертикальной исходной площадкой равны:
с вертикальной исходной площадкой равны:
 450, получаем
450, получаем 
 , получаем
, получаем
 (рис. 18).
(рис. 18). называется абсолютным сдвигом. Отношение абсолютного сдвига
называется абсолютным сдвигом. Отношение абсолютного сдвига 

 пропорционален касательным напряжениям. Математическая зависимость между углом сдвига и касательным напряжением называется законом Гука при сдвиге.
пропорционален касательным напряжениям. Математическая зависимость между углом сдвига и касательным напряжением называется законом Гука при сдвиге.
 коэффициент пропорциональности или модуль упругости второго рода.
коэффициент пропорциональности или модуль упругости второго рода.
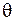 не зависит от того, как в окрестности точки выделен элементарный параллелепипед. Так как при чистом сдвиге боковые грани выделенного элементарного параллелепипеда являются площадками чистого сдвига, то
не зависит от того, как в окрестности точки выделен элементарный параллелепипед. Так как при чистом сдвиге боковые грани выделенного элементарного параллелепипеда являются площадками чистого сдвига, то 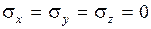 . Тогда относительное изменение объёма при чистом сдвиги
. Тогда относительное изменение объёма при чистом сдвиги  .
. равна сумме удельной потенциальной энергии изменения объёма
равна сумме удельной потенциальной энергии изменения объёма  и удельной потенциальной энергии изменения формы
и удельной потенциальной энергии изменения формы 

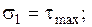
 , получаем
, получаем

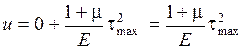 .
.
 сила, действующая на грань параллелепипеда.
сила, действующая на грань параллелепипеда.
 размер параллелепипеда в направлении, перпендикулярном чертежу (рис. 18)
размер параллелепипеда в направлении, перпендикулярном чертежу (рис. 18) получаем
получаем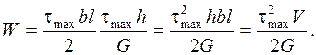
 .
.
 =
=  ,
, и модулем упругости второго рода
и модулем упругости второго рода 
 .
.


