Лекция 2. Растяжение – сжатие
Нормальная сила. При растяжении или сжатие в поперечных сечениях бруса возникает только один внутренний силовой фактор – нормальная сила Составим условие равновесия на ось
Проведем на втором участке сечение на расстоянии Нормальные напряжения. Исходя из определения напряжения, можно записать
где Согласно гипотезе Бернулли (гипотеза плоских сечений) все продольные волокна бруса деформируются одинаково, а это означает, что напряжения в поперечных сечениях одинаковы, т.е. В этом случае получаем
Рассчитывая напряжения в каждом сечении, строим эпюру нормальных напряжений.
Перемещения и деформации. При растяжении бруса длиной Величина О степени деформирования бруса нельзя судить по значениям
начальных размеров бруса. Для характеристики деформации бруса вводятся понятия относительная продольная деформация
Отношение Для большинства материалов в стадии упругой деформации выполняется соотношение, представляющее собой математическое выражение закона Гука
где Подставляя в выражение закона Гука
Произведение Определяя перемещения каждого сечения, строим эпюру продольных перемещений сечений бруса (рис. 3).
|

 (рис. 3). Брус имеет два характерных участка. Для определения нормальной силы
(рис. 3). Брус имеет два характерных участка. Для определения нормальной силы  проведем сечение на первом участке и рассмотрим равновесие отсеченной части (рис. 4). Нормальную силу будем всегда показывать от сечения, что будет соответствовать растяжению бруса.
проведем сечение на первом участке и рассмотрим равновесие отсеченной части (рис. 4). Нормальную силу будем всегда показывать от сечения, что будет соответствовать растяжению бруса.

 . Рассматривая равновесие отсеченной части, получаем
. Рассматривая равновесие отсеченной части, получаем 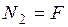 . Строим эпюру нормальных сил.
. Строим эпюру нормальных сил. Рис. 4
Рис. 4 ,
, нормальное напряжение в произвольной точке сечения.
нормальное напряжение в произвольной точке сечения.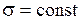 .
. , откуда
, откуда  .
.
 его длина увеличивается на величину
его длина увеличивается на величину  , а его диаметр
, а его диаметр  уменьшается на величину
уменьшается на величину  (рис.5).
(рис.5). абсолютной поперечной деформацией.
абсолютной поперечной деформацией. Рис.5
Рис.5 и относительная поперечная деформация
и относительная поперечная деформация  , которые рассчитываются по зависимостям
, которые рассчитываются по зависимостям
 называется коэффициентом поперечной деформации или коэффициентом Пуассона.
называется коэффициентом поперечной деформации или коэффициентом Пуассона.
 коэффициент пропорциональности, который получил название модуля упругости первого рода.
коэффициент пропорциональности, который получил название модуля упругости первого рода. и
и  откуда
откуда 
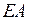 называется жесткостью бруса при растяжении (сжатии).
называется жесткостью бруса при растяжении (сжатии).



