Лекция 4. Теория напряженного состояния
Вырежем из напряженного тела в окрестности исследуемой точки произвольно бесконечно малый параллелепипед. На гранях параллелепипеда будут действовать нормальные и касательные напряжения. Направление нормальных напряжений совпадает с направлением внешней нормали. Касательные напряжения разложим на составляющие, параллельные осям. Напряженным состоянием тела в точке называют совокупность нормальных и касательных напряжений, действующих по всем площадкам содержащим данную точку. Обозначения нормальных напряжений содержат один индекс - наименование оси, которой параллельно данное напряжение. В обозначении касательных напряжений используются два индекса: первый совпадает с индексом нормального напряжения, действующего по данной площадке, а второй - наименование оси, которой параллельно данное касательное напряжение.
Рис. 11 Нормальное напряжение
Рис.12
Закон парности касательных напряжений. Закон парности касательных напряжений устанавливает зависимость между величинами и направлениями пар касательных напряжений, действующих по взаимно перпендикулярным площадкам элементарного параллелепипеда. Рассмотрим элементарный параллелепипед размеров dx, dy, dz (рис. 12). Запишем уравнение равновесия параллелепипеда в виде суммы моментов относительно оси
Аналогично можно получить Это и есть закон парности касательных напряжений. Касательные напряжения по двум взаимно перпендикулярным площадкам равны по величине и противоположны по знаку. Главные площадки и главные напряжения. Рассмотрим две взаимно-перпендикулярные площадки с касательными напряжениями Площадки, по которым касательные напряжения равны нулю, называются главными, а действующие по этим площадкам нормальные напряжения - главными напряжениями. Главные напряжения обозначаются
Рис. 13
Виды напряженного состояния тела. В зависимости от количества действующих главных напряжений различают три вида напряженных состояний: линейное, плоское и объемное.
Линейное напряженное состояние. Определим напряжения, возникающие в наклонном сечении За положительное направление отсчетов угла В общем случае в наклонном сечении будут действовать как нормальные напряжения Их значения определим из условия равновесия нижней части. Проектируя силы на направления
учитывая, что
Рис.15
Из суммы проекций сил на направления
Плоское напряженное состояние. Плоским или двухосным называется напряженное состояние, при котором одно из трех главных напряжений равно нулю (рис. 14, б). Для плоского напряженного состояния различают две задачи – прямую и обратную. В прямой задаче гранями рассматриваемого элемента являются главные площадки (рис. 16, а). Известны s1¹ 0, s2¹ 0, s3 = 0 и требуется определить напряжения sa и ta и sb и tb на произвольных площадках. В обратной задаче известны напряжения на двух взаимно произвольных перпендикулярных площадках sx, sy, tyx и txy и требуется определить положение главных площадок и величины главных напряжений.
Прямая задача. Для решения этой задачи воспользуемся принципом независимости действия сил. Представим плоское напряженное состояние в виде суммы двух независимых линейных напряженных состояний: первое – при действии только напряжений
Таким образом, суммируя напряжения, возникшие при каждом линейном напряженном состоянии, получим
Определим напряжения, действующие на площадку с углом наклона
Суммируя нормальные напряжения, действующие по произвольным взаимно перпендикулярным площадкам, получим
Сравнивая величины касательных напряжений, имеем
Обратная задача. Определим сначала напряжения на наклонной площадке, наклоненной к исходной, при заданныхнапряжения на двух взаимно произвольных перпендикулярных площадках sx, sy, tyx и txy (рис. 16, б). Разрежем параллелепипед плоскостью, наклоненной под углом Если обозначить через Спроектируем силы на направления
Сокращая на
Для отыскания экстремального значения нормального напряжения продифференцируем
Экстремум напряжения Предполагая, что главные площадки наклонены к исходным площадкам на угол
Полученному равенству удовлетворяют два значения угла Модули главных напряжений определяют по зависимости:
Объемное напряженное состояние. Объемным или трехосным называется напряженное состояние, при котором все три главных напряжения отличны от нуля (рис. 14, в). Для объемного напряженного состояния справедливо равенство
Обобщенный закон Гука. Обобщенный закон Гука представляет собой связь между напряжениями и деформациями в случае объемного. Он может быть получен на основании закона Гука для линейного напряженного состояния и принципа независимости действия сил. Представляя объемное напряженное состояние в виде суммы трех линейных напряженных состояний, и учитывая, что при линейном напряженном состоянии
Эти выражения носят название обобщенного закона Гука, записанного для главных площадок. Деформации e1, e2 и e3, в направлении главных напряжений называются главными деформациями.
|


 считается положительным, если оно направлено от площадки. Касательное напряжение
считается положительным, если оно направлено от площадки. Касательное напряжение  считается положительными, если изображающий его вектор стремится вращать параллелепипед по часовой стрелки относительно любой точке, лежащей внутри параллелепипеда. Отрицательными считаются напряжения обратных направлений.
считается положительными, если изображающий его вектор стремится вращать параллелепипед по часовой стрелки относительно любой точке, лежащей внутри параллелепипеда. Отрицательными считаются напряжения обратных направлений.
 , получим:
, получим:
 откуда получаем
откуда получаем 

 и
и  . Согласно закону парности касательных напряжений знаки
. Согласно закону парности касательных напряжений знаки  .
. , причем
, причем  . Элемент, выделенный главными площадками, изображен на рис. 13.
. Элемент, выделенный главными площадками, изображен на рис. 13.

 Линейным или одноосным называется напряженное состояние, при котором два из трех главных напряжений равны нулю (рис.14, а).
Линейным или одноосным называется напряженное состояние, при котором два из трех главных напряжений равны нулю (рис.14, а).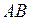 , нормаль к которому повернута на угол
, нормаль к которому повернута на угол  к направлению
к направлению  .
. , так и касательные напряжения
, так и касательные напряжения  .
.
 получаем
получаем 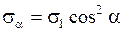 .
.

 Рис. 16
Рис. 16 . От каждого из напряжений
. От каждого из напряжений 

 , то есть перпендикулярную к площадке
, то есть перпендикулярную к площадке 
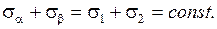

 площадь наклонной грани, то площади вертикальной и горизонтальной граней будут соответственно равны
площадь наклонной грани, то площади вертикальной и горизонтальной граней будут соответственно равны  и
и  .
.
 , получаем
, получаем

 . Отсюда следует, что нормальные напряжения достигают экстремума на тех площадках, где касательные ускорения обращаются в нуль. Эти площадки называются главными, а напряжения, возникающие на них – главными напряжениями.
. Отсюда следует, что нормальные напряжения достигают экстремума на тех площадках, где касательные ускорения обращаются в нуль. Эти площадки называются главными, а напряжения, возникающие на них – главными напряжениями. , получаем
, получаем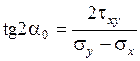 .
. .
. .
. и
и 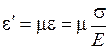 , выражения для деформации в направлении действия главных напряжений будут иметь вид:
, выражения для деформации в направлении действия главных напряжений будут иметь вид:



