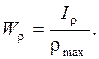Лекция 3. Геометрические характеристики плоских сечений
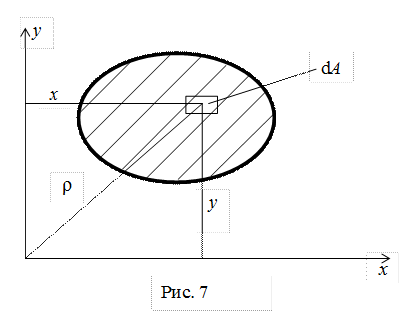
Статические моменты сечения. Любое сечение бруса имеет определенную геометрическую форму и площадь (рис.7). Выделим в сечение элементарную площадку площадки на расстояние до оси. Статические моменты сечения относительно осей x и y будут соответственно равны
Определение центра тяжести сечения. Статические моменты сечения относительно осей проходящих через центр тяжести равны нулю, поэтому их используют для определения координат центров тяжести сечения. Для этого проводят вспомогательные оси x и y и координаты центра тяжести сечения определяют по зависимостям:
Моменты инерции сечения. Осевым моментом инерции сечения
Полярным моментом инерции сечения
Учитывая, что Полярный момент инерции сечения равен сумме осевых моментов инерции сечения. Центробежным моментом инерции сечения
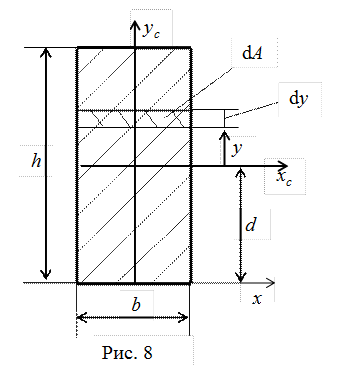
Если сечение имеет ось симметрии, то центробежный момент инерции сечения равен нулю. Определение моментов инерции простых геометрических фигур. Рассмотрим определения момента инерции прямоугольного сечения относительно оси, проходящей через центр тяжести (рис. 8). Выделим элементарную площадь
В нашем случае элементарная площадь
Аналогичным образом определяются моменты инерции плоского сечения.
Рис.9 Если известен момент инерции сечения относительно оси проходящей через центр тяжести (рис. 9), то момент инерции относительно другой параллельной оси, отстоящей на расстоянии
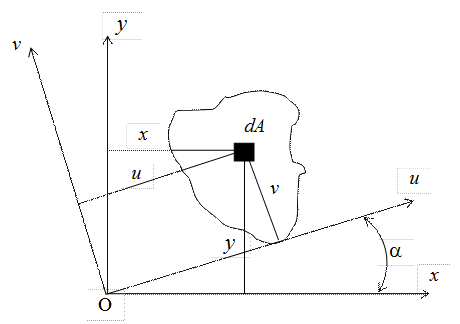
Если сечение имеет сложную геометрическую форму, то его разбивают на простые фигуры и его момент инерции рассчитывают, как сумму моментов инерции отдельных фигур. Найдем зависимость между моментами инерции относительно осей х, у и моментами инерции относительно осей u, v, повернутых на угол Из рисунка следует:
Рис. 10 В этом случае
Главные оси инерции и главные моменты инерции. С изменением угла поворота осей
откуда
Нетрудно показать, что центробежный момент относительно осей, повернутых на угол Оси, относительно которых центробежный момент инерции равен нулю, а осевые моменты инерции принимают экстремальные значения, называются главными осями. Если эти оси являются также и центральными, то они называются главными центральными осями. Осевые моменты инерции относительно главных осей называются главными моментами инерции. Если сечение имеет ось симметрии, то эта ось всегда является одной из главных центральных осей инерции сечения. Момент сопротивления сечения. Момент сопротивления сечения относительно оси представляет собой отношение момента инерции относительно данной оси к расстоянию до наиболее удаленной точки сечения от этой же оси.
Момент сопротивления прямоугольного сечения, изображенного на рис. 8, относительно оси, проходящей через центр тяжести, равен
Полярный момент инерции представляет собой отношение полярного момента инерции к наибольшему расстоянию от центра тяжести сечения до наиболее удаленной точки сечения
|

 , положение которой определено координатами x и y. Статическим моментом сечения
, положение которой определено координатами x и y. Статическим моментом сечения  называется интеграл по площади произведения элементарной
называется интеграл по площади произведения элементарной
 .
.
 называется интеграл по площади произведения элементарной площадки на квадрат расстояния до оси. Осевые моменты инерции сечения относительно осей x и y будут соответственно равны
называется интеграл по площади произведения элементарной площадки на квадрат расстояния до оси. Осевые моменты инерции сечения относительно осей x и y будут соответственно равны
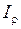 называется интеграл по площади произведения элементарной площадки на квадрат расстояния до начало координат.
называется интеграл по площади произведения элементарной площадки на квадрат расстояния до начало координат.
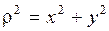 , получаем
, получаем 
 называется интеграл по площади произведения элементарной площадки на расстояния до осей.
называется интеграл по площади произведения элементарной площадки на расстояния до осей.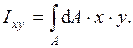
 от центральной оси
от центральной оси  толщиной
толщиной 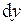 . Согласно определению, осевой момент инерции относительно оси
. Согласно определению, осевой момент инерции относительно оси 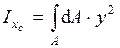 .
.
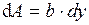 . Подставляя значения
. Подставляя значения 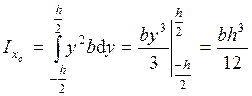 .
.
 , определяется по формуле Штейнера
, определяется по формуле Штейнера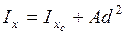 .
. . Угол
. Угол  .
.

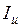 и
и 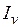 меняется, а сумма их остается неизменной. Следовательно, существует такое значение
меняется, а сумма их остается неизменной. Следовательно, существует такое значение 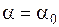 , при котором моменты инерции достигают экстремальных значений, т.е. один из моментов инерции достигает своего максимального значения, в то время другой момент инерции принимает минимальное значение. Для нахождения значения
, при котором моменты инерции достигают экстремальных значений, т.е. один из моментов инерции достигает своего максимального значения, в то время другой момент инерции принимает минимальное значение. Для нахождения значения  возьмем первую производную от
возьмем первую производную от 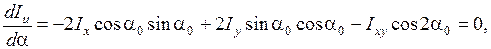

 .
.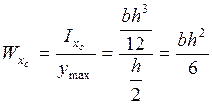 .
.