Устойчивые и неустойчивые формы равновесия
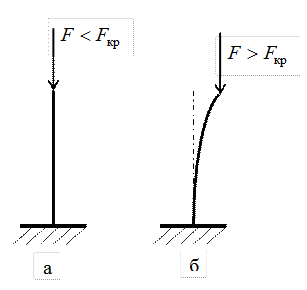
Соблюдение условий прочности и жесткости еще не гарантирует способности конструкций выполнять, предназначенные им функции в эксплуатационных режимах. Наряду с выполнением условий прочности и жесткости, необходимо обеспечить и устойчивость конструкций. При неизменной схеме нагружения, под устойчивостью понимается свойство способности системы сохранять свое первоначальное равновесное состояние. Значения внешних сил, при которых происходит потеря устойчивости, называются критическими. Рассмотрим длинный тонкий стержень (рис. 30, а) нагруженный осевой сжимающей силой Если увеличить сжимающую силу Значение силы, при которой первоначальная форма равновесия упругого тела становится неустойчивой, называется критической силой. Наименьшее значение сжимающей силы, при котором сжатый стержень теряет способность сохранять прямолинейную форму устойчивого равновесия, так же называют критической силой и обозначают
Рис. 30
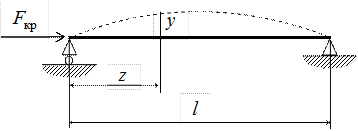
Определение критической силы. Формула Эйлера. Рассмотрим решение задачи об устойчивости сжатого стержня силой
Рис. 31 Записывая дифференциальное уравнение упругой линии балки, и ограничиваясь рассмотрением только малых перемещений, имеем:
где Изгибающий момент Mx (z), действующий в поперечном сечении стержня, расположенного на расстоянии z от начала системы координат, будет равен
При положительном прогибе в выбранной системе координат знак “минус” означает, что момент является отрицательным. Дифференциальное уравнение изогнутой оси балки в направлении минимальной жесткости в этом случае будет иметь вид:
Обозначая
Общее решение данного уравнения имеет вид
где A и B – постоянные интегрирования. Постоянные интегрирования определяем из условий равенства нулю прогибов стержня на опорах. В этом случае имеем: при z=0, y=0, A =0; z = l, y= 0,
Откуда
Минимальное действительное значение критической силы получится при n= 1.
Это и есть формула Эйлера для определения критической силы. Влияние способов закрепления концов стержня на критическую силу. Формула Эйлера получена для случая шарнирного закрепления концов стержня, когда потеря устойчивости происходит по одной полуволне. Для других случаев закрепления формула Эйлера принимает вид
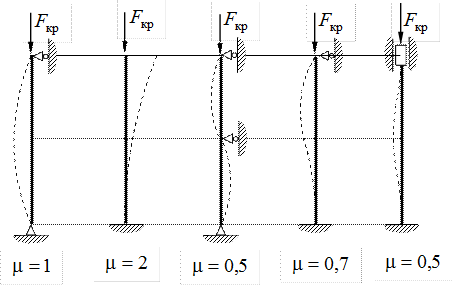
где μ – коэффициент приведения длины, зависящий от способа закрепления концов стержня (рис. 32).
Рис. 32
Критические напряжения равны
где
Пределы применимости формулы Эйлера. При выводе формулы для критических сил и напряжений, использовалось приближенное дифференциальное уравнение изогнутой оси балки, которое было получено в предположении, что материал стержня подчиняется закону Гука. Таким образом, формулу Эйлера можно применять только для значений напряжений, меньших или равных пределу пропорциональности
откуда
В случаях, когда гибкость стержня
где
|

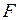 . В этом случае возможны две формы равновесия стержня: прямолинейная и криволинейная. При малых значениях силы
. В этом случае возможны две формы равновесия стержня: прямолинейная и криволинейная. При малых значениях силы 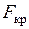 .
.
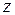 прогиб составил
прогиб составил  .
.
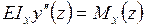 ,
,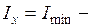 минимальный момент инерции сечения.
минимальный момент инерции сечения.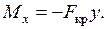
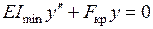 .
.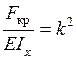 , получим линейное дифференциальное уравнение второго порядка относительно прогиба
, получим линейное дифференциальное уравнение второго порядка относительно прогиба 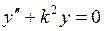
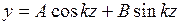
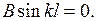 Последнее соотношение справедливо при
Последнее соотношение справедливо при 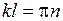 (n – любое целое число).
(n – любое целое число).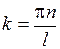 , с учетом принятого ранее обозначения, получим
, с учетом принятого ранее обозначения, получим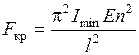 .
.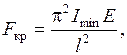
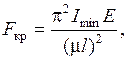
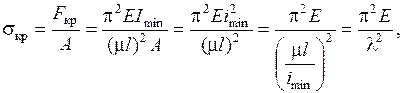
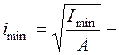 минимальный радиус инерции;
минимальный радиус инерции;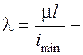 гибкость стержня.
гибкость стержня.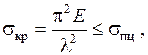
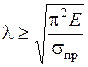 . Таким образом, формула Эйлера может применяться при условии, что
. Таким образом, формула Эйлера может применяться при условии, что 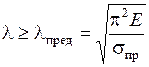 .
.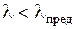 критическое напряжение определяется по эмпирическим зависимостям. В частности, Ф.С. Ясинский предложил следующую формулу для критических по устойчивости напряжений:
критическое напряжение определяется по эмпирическим зависимостям. В частности, Ф.С. Ясинский предложил следующую формулу для критических по устойчивости напряжений: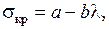
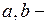 постоянные величины, зависящие от материала стержня.
постоянные величины, зависящие от материала стержня.


